De som van de afstanden tot twee vaste punten F1
en F2 (de brandpunten) is constant.
|
Vergelijking van een
ellips
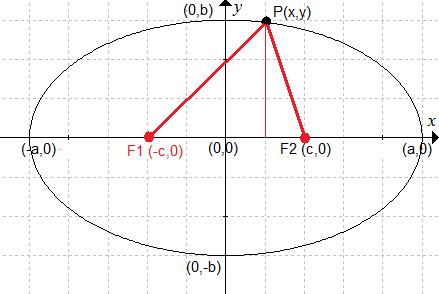
We passen de omschrijving van de meetkundige plaats toe op onderstaande
tekening.
De afstand tussen gegeven punten F1 en F2 = 2c
De som van de afstanden van een punt P(x,y) op de ellips tot de punten F1
en F2 = 2a..
Voor een willekeurig punt P op de ellips vinden we met de hulp van Pythagoras:
de afstand tussen de punten P en F1 =
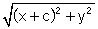
de afstand tussen de punten P en F2 =
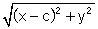
De som van beide afstanden moet gelijk zijn aan 2a, zodat:
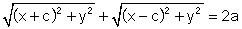
Door kwadrateren en herschikken van termen kunnen we deze voorwaarde
omvormen.
Als algemene vergelijking van een ellips vinden we zo:
|
a vinden we terug als de
afstand die op de x-as wordt afgesneden.
b vinden we terug als de afstand die op de y-as wordt
afgesneden.
c is de halve afstand tussen de brandpunten en voldoet aan de
vergelijking c² = a² - b²
|
Een ellips met samenvallende brandpunten wordt een cirkel.
Die verkrijgen we door op de x-as en
de y-as gelijke afstanden af te snijden.
(a = b = de straal r van de cirkel).
Voor de vergelijking van de cirkel betekent dat:
x² + y² = r²
En deze vergelijking herken je natuurlijk als de vergelijking van
een cirkel met de oorsprong als middelpunt.
Ellipspasser:
De Nederlandse wiskundige Frans van Schooten ontwierp in de 17e eeuw
een ellipspasser.
In een vierkante grondplaat worden haaks op elkaar twee kruisende
sleuven gemaakt.
In de twee sleuven ligt een glijdend klosje. Op de klosjes wordt een
lat bevestigd, die de klosjes verbindt.
Aan het eind van de lat is een potlood bevestigt waarmee de ellips
getekend wordt.
hyperbool
Een hyperbool is de meetkundige plaats van de punten met
volgende eigenschap:
Het verschil van de afstanden tot twee vaste punten F1
en F2 (de brandpunten) is constant.
|
Vergelijking van een
hyperbool
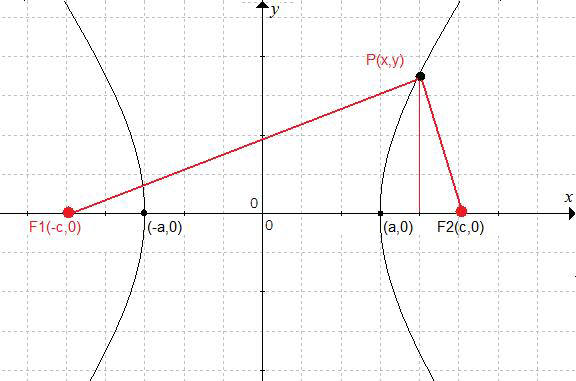
We passen de omschrijving van de meetkundige plaats toe op onderstaande
tekening.
De afstand tussen gegeven punten F1 en F2 = 2c
Het verschil van de afstanden van een punt P(x,y) op de hyperbool tot de punten
F1 en F2 = 2a..
Voor een willekeurig punt P op de hyperbool vinden we met de hulp van
Pythagoras:
de afstand tussen de punten P en F1 =
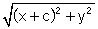
de afstand tussen de punten P en F2 =
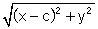
Het verschil van beide afstanden moet gelijk zijn aan 2a, zodat:
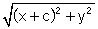 -
-
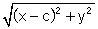 =
2a
=
2a
Verder uitwerken van deze voorwaarde levert volgende algemene
vergelijking op:
|
a vinden we terug als de
afstand die de twee takken op de x-as afsnijden.
c is de halve afstand tussen de brandpunten en voldoet aan de
vergelijking c² = a² + b²
|
algemene vergelijking van een kegelsnede
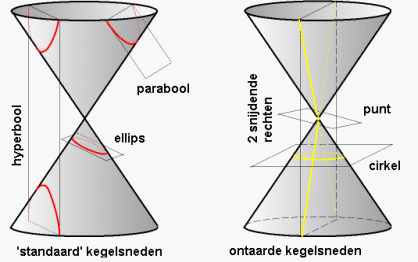 |
wanneer we een dubbele kegel snijden door een vlak
verschijnen parabolen, ellipsen en hyperbolen.
We noemen ze daarom kegelsneden.
Wanneer het snijdend vlak door de top van de kegel gaat,
is het resultaat een punt of 2 snijdende rechten.
We spreken dan van ontaarde kegelsneden. |
De verschillende types van kegelsneden kunnen we in één algemene
vergelijking schrijven.
In een cartesiaans assenstelstel is een kegelsnede altijd van de vorm
ax² + h xy + b y² + 2g x + 2f y + c = 0, een
kwadratische vergelijking in twee variabelen x
en y.
als h2 = ab, stelt de vergelijking een
parabool
voor;
als h2 < ab, stelt de vergelijking een
ellips voor;
als h2 > ab, stelt de vergelijking een
hyperbool
voor;
als a = b en h = 0, stelt de vergelijking een
cirkel
voor;
als a + b = 0, stelt het een rechthoekige
hyperbool voor.
als b =f = 0, dan ontaardt de kegelsnede in
twee snijdende rechten,
als c =0, dan ontaardt de kegelsnede in een punt.