De Gulden Snede

een bijzondere verdeling
Een lengte kunnen we volgens dezelfde verhouding opdelen in en kort en lang stuk.
Er is echter een verdeling, zo dat het langste stuk middelevenredig is tussen het hele lijnstuk en het kleinste stuk.
We spreken dan van de Gulden Snede.
Je kan experimenteren in volgend applet, om deze verhouding te zoeken:

We spreken van een gulden rechthoek als de langste zijde van een rechthoek middelevenredig is
tussen de som van beide zijden en de kortste zijde.
In formulevorm wordt dit:

berekening van deze verhouding
Door te experimenteren in het applet kunnen we deze verhouding benaderen, maar hoe berekenen we ze?

som van de twee zijden	=	langste zijde
langste zijde	=	kortste zijde

We nemen een rechthoek met als kortste zijde 1.
Hoe lang is dan de langste zijde?
Hiervoor moeten we een vierkantsvergelijking oplossen:

x + 1	=	x
x	=	1

x² = x + 1
x² - x - 1 = 0
D = 1 - 4 . (1).(-1) = 5

x₁ =	1 + √5	= 1,618
	2
x₂ =	1 - √5	= - 0,618
	2

De lengte van een rechthoek kan niet negatief zijn.
De gevraagde lengte is gelijk aan 1,6180339887499.

Dit getal duidt men aan met de Griekse letter FI (Φ).

Deze Fi is een van de vele wiskundige eigenaardigheden die wiskunde boeiend maken.
De verhouding duikt op de meest onverwachte plaatsen op, maar ook rekenkundig is ze merkwaardig:

constructie
Er bestaat ook een meetkundige constructie om een gulden rechthoek te construeren:

De Oude Grieken hechtten veel belang aan harmonieuze verhoudingen.
Pythagoras zocht naar harmonieuze verhoudingen in de natuur.
Polycletos legde voor de beeldhouwers de precieze verhoudingen van hoofd en lichaam vast in een canon.
Ook de verhouding van de gulden snede was gekend bij wiskundigen en kunstenaars.

	De verhouding van de lengtes van hand en voorarm zou overeenkomen met de gulden snede
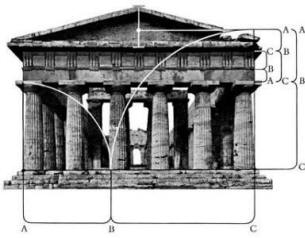	foto van de Posseidontempel nabij Napels
Vaak vind je dezelfde tekening en foto, en gulden snede-fanaten zien de verhouding zowat overal in Griekse tempels opduiken, in hoofdverhoudingen en details. Helaas ziet men meestal slechts wat men wil zien. De foto van de Posseidontempel is een mooi voorbeeld: Onderaan valt de snede aan de linkerkant van de derde zuil ... ze moet natuurlijk ergens vallen, maar dit is geen merkwaardig punt in de tempel. Wie zou net daar een harmonieuze verhouding leggen? Bovenaan is het nog merkwaardiger: men tekent een punt gewoon in het midden van het driehoekig fronton ... Zo is het niet moeilijk om een gebouw vol te tekenen met gulden snede verhoudingen. Het lukt je vast ook wel met je eigen huis of schoolgebouw. Auteurs die in het Parthenon de verhouding 9 /4 terugvinden lijken dan ook geloofwaardiger dan Φ-speurders die op pseudo-wetenschappelijke websites hun hun kosmische bevindingen tentoonspreiden. Het Parthenon werd trouwens gebouwd ca 440 v.Chr., terwijl Eudoxus over de verhouding schreef rond 370 v.Chr. en Euclides leefde van 323 tot 283 v.Chr.
Een verkenning van het internet illustreert hoe ver sommigen gaan in hun zoektocht om zowat overal de gulden snede te zien: Een poort in een Mayatempel: we tekenen de rechthoek wel even door tot de rand van de overgebleven muur, en ja hoor! Een vette lijn corrigeert zelfs een foto met schuine lijnen... De Mona Lisa mag natuurlijk niet ontbreken in het mysterieuze rijtje. Maar vind je ook niet dat de rechthoeken wel heel willekeurig getekend lijken? "Se non é vero, é ben trovato" zegt men in het Italiaans. (Is het niet waar, dan is het toch goedgevonden...)

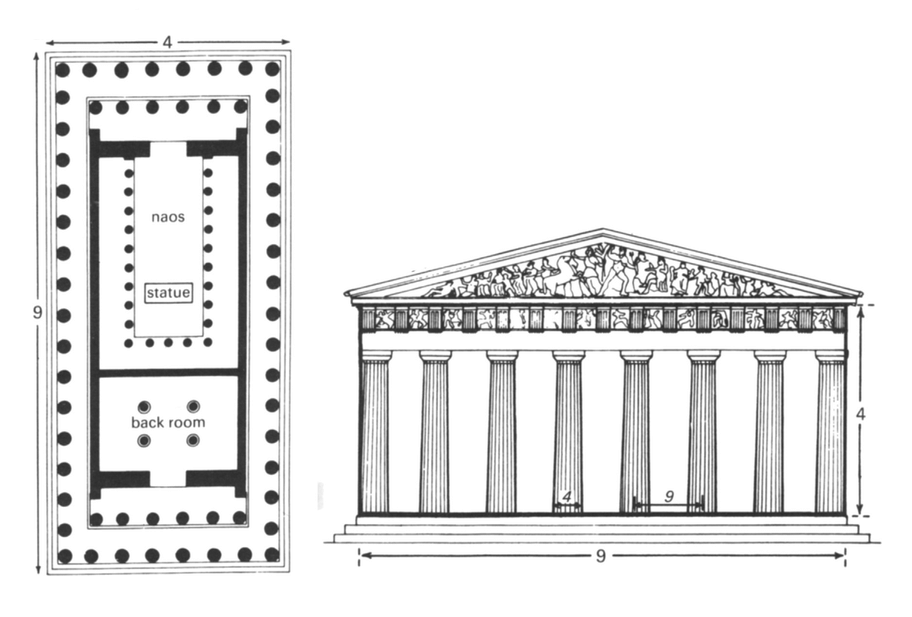
Het Parthenon en de verhouding 9:6::6:4
Een verhouding die je wel terugvindt in het Parthenon is de verhouding 9:4.
Met de middelevenredige 6 daarbij krijg je de verhouding 9:6::6:4.
9:6 = 6:4 = 3:2 en deze 3:2 verhouding is wel een klassieker in de Griekse Oudheid.
Reeds in de 6e eeuw v.Chr. gebruikte Pythagoras deze verhouding om een toonladder op te bouwen.
We kennen ze nog steeds als een reine kwint (bv.: do-sol).

De verhouding 9:4 komt overeen met de verhouding lengte:breedte.
Ook de rechthoek tussen podium onderaan en triforium bovenaan is een rechthoek met verhouding 9:4.

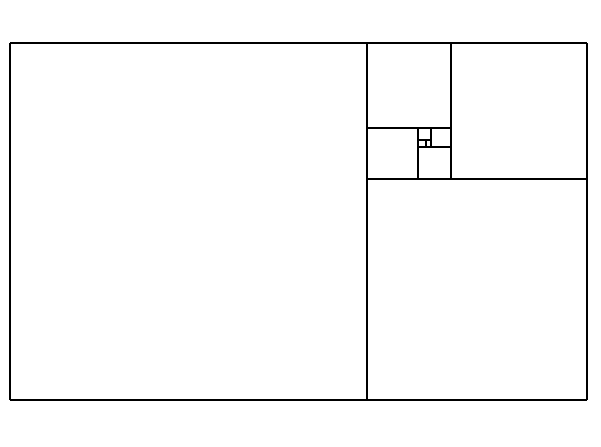
de gulden snede en de rij van Fibonacci
We stapelen spiraalsgewijs steeds groter wordende vierkanten, waarbij de lengte van de zijden overeenkomt
met de rij van Fibonacci: (1)1 2 3 5 8 13 21 34 ...
De vierkanten vormen gulden rechthoeken.
Op het internet hoef je maar 'golden section' of 'Fibonacci' in te typen om een massa sites te vinden.