eerstegraadsfuncties

Algemeen:

Een functie bereikt een extremum wanneer de afgeleide verandert van teken.
Afgeleide wordt hierdoor een instrument om problemen op te lossen in de aard van:
"Wanneer wordt ... maximaal/minimaal?"
We moeten hierbij een concreet probleem wel kunnen vertalen in een functievoorschrift.
Hoe kan je hierbij te werk gaan?

- Een tekening maken kan je meer inzicht geven in de situatie

- Reken enkele cijfervoorbeelden uit.
    Je krijgt zo een beter idee hoe het probleem wiskundig in elkaar zit.

- Probeer nu de stap te maken naar een onbekende x:
    x = de grootheid die er voor moet zorgen dat een andere grootheid maximaal/minimaal wordt.
    (Zijn er meer onbekenden, dan is er steeds een extra gegeven, waaruit je een verband tussen de onbekenden kunt afleiden.
      Noem één onbekende x en druk de andere uit in functie van x.)

- Schrijf nu het algemene functievoorschrift op, met hierin de veranderlijke x

- Bereken de afgeleide functie

- Bereken de nulpunten van de afgeleide functie en maak het tekenoverzicht van de afgeleide functie

- Lees het gevraagde maximum/minimum af

- controleer nu het gevonden resultaat aan de hand van de oorspronkelijke opgave
    (en niet aan de hand van je functievoorschrift, want dat kan zelf fout zijn!)

Verdeel het getal 120 in twee positieve getallen,
zo dat het product van het kwadraat van het eerste getal met het tweede getal maximaal is.

naar oplossing

Verdeel het getal 60 in twee positieve getallen,
zo dat som van de kwadraten van de twee getallen minimaal is.

naar oplossing

Een plaat van 1m breed plooi je, zo dat ze een goot vormt.
Bij welke afmetingen kan door de goot een maximale hoeveelheid water stromen?

naar oplossing

Uit een vierkant van 40x40cm knip je vierkantjes. Zo kan je het geheel plooien tot een doos.
Hoeveel knip je weg om een zo groot mogelijke doos te bekomen?

naar oplossing

Je moet een doos inpakken met een lint van 2m lang. De afmetingen van de doos mag je zelf kiezen.
Bepaal de afmetingen om een zo groot mogelijke doos te kunnen inpakken.

naar oplossing

Een sportstadion bestaat uit een rechthoek met twee halve cirkels en heeft een omtrek van van 400m.
Bepaal de afmetingen van het stadion zo dat het centrale rechthoekige sportveld maximaal wordt.

naar oplossing

Uit een boomstam met een diameter van 30cm wordt een rechthoekige balk gezaagd.
Het draagvermogen van zo'n balk hangt natuurlijk af van de hoogte en de breedte van de balk
en is evenredig met het product b.h².
Bepaal de afmetingen van de balk zo dat het draagvermogen zo groot mogelijk wordt.

naar oplossing

cilinder in kegel
In een kegel met straal 4cm en een hoogte van 6cm plaats je een cilinder.
Voor welke afmetingen wordt de inhoud van de cilinder maximaal?

naar oplossing

rekenvoorbeelden:
Als het eerste getal 5 is, is het tweede getal 120 - 5 = 115.
Het product wordt: 5² . (115) = 2875

Als het eerste getal 10 is, is het tweede getal 120 - 10 = 110.
Het product wordt: 10² . (110) = 11000

van rekenvoorbeeld naar een onbekende x:
Als het eerste getal x is, is het tweede getal 120 - x.
Het product wordt: x² . (120 - x) = 120x² - x³

berekenen:
Het product dat maximaal moet zijn, vinden we als:
P(x) = - x³ + 120x².
Voor een maximale waarde moet de afgeleide 0 worden.
De afgeleide functie wordt dan: P ' (x) = -3x² + 240x.
We vinden:
-3x² + 240x = 0
3x (- x + 80) = 0
x = 0 of x = 80.

P ' (x) - 0 + 0 -
P (x) ↘ min ↗ max ↘

Het zinvol domein = [ 0 , 120 ]

Als oplossing vinden we:
Het ene getal = x = 80
Het andere getal = 120 - x = 40

controle:
Ga nu in het applet na of het product inderdaad maximaal is als we als eerste getal 80 nemen.

rekenvoorbeelden:
Als het ene getal 5 is, is het andere getal 60 - 5 = 55.
De gevraagde som wordt: 5² + 55² = 3050

Als het ene getal 10 is, is het andere getal 60 - 10 = 50.
De gevraagde som wordt: 10² + 50² = 2600

van rekenvoorbeeld naar een onbekende x:
Als het ene getal x is, is het andere getal 60 - x.
De gevraagde som wordt: x² + (60 - x)² = x² +3600 - 120x + x² = 2x² - 120x + 3600

berekenen:
De som die minimaal moet zijn, vinden we als:
S(x) = 2x² - 120x + 3600.
Voor een minimale waarde moet de afgeleide 0 worden.
De afgeleide functie wordt dan: S ' (x) = 4x - 120.
We vinden:
4x - 120 = 0
4x = 120
x = 30.

Als oplossing vinden we:
Het ene getal = x = 30
Het andere getal = 60 - x = 30

controle:
De som van 30 en 30 is inderdaad 60.
Ga nu in het applet na of de som inderdaad minimaal is als we als getallen 30 en 30 nemen.

maak eerst een schets:

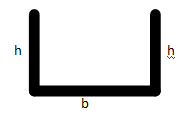
rekenvoorbeelden:
Als de hoogte 20cm is, is de breedte 100 - 2 . 20 = 60.
De doorsnede van de goot heeft een oppervlakte van 20 . 60 = 1200 cm²

Als de hoogte 10cm is, is de breedte 100 - 2 .
De doorsnede van de goot heeft een oppervlakte van 20 . 60 = 1200 cm²

Als de hoogte 10cm is, is de breedte 100 - 2 . 10 = 80.
De doorsnede van de goot heeft een oppervlakte van 10 . 80 = 800 cm²

van rekenvoorbeeld naar een onbekende x:
Als de hoogte x is, is het andere getal 100 - 2x.
De oppervlakte wordt: x . (100 - 2x) = 100x - 2x²

berekenen:
De oppervlakte die maximaal moet zijn, vinden we als:
O(x) = - 2x? + 100x.
Voor een maximale waarde moet de afgeleide 0 worden.
De afgeleide functie wordt dan: O ' (x) = -4x + 100.
We vinden:
4x = 100
x = 25.

x                                                   25

O ' (x) = - x + 80              +           0         -
O (x)                    ↗      max ↘

Het zinvol domein = [ 0 , 50 ] want 2 keer 50cm is de plaat al opgebruikt.100cm, wat klopt met het gegeven.
Ga nu in het applet na of de oppervlakte inderdaad maximaal wordt voor een hoogte van 25cm.

oplossing vierkantjes knippen

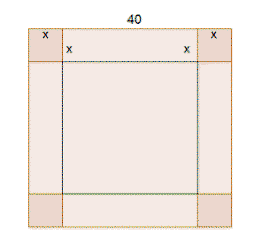
We weten: de inhoud van een balkvormige doos = l . b . h
Het grondvlak is een vierkant, dus l = b

enkele rekenvoorbeelden:

Als je aan de twee kanten 2 cm afknipt, wordt de zijde van de doos: 40 - 2 . 2 = 36 cm.
Deze 2 cm wordt de hoogte.
De inhoud van de doos wordt dus 36 . 36 . 2 = 2592 cm².

Als je aan de twee kanten 4 cm afknipt, wordt de zijde van de doos: 40 - 2 . 4 = 32 cm
Deze 4 cm wordt de hoogte.
De inhoud van de doos wordt dus 32 . 32 . 4 = 4096 cm².

De inhoud van de doos wordt groter.
We kunnen nu verder gaan en zien of dat zo blijft.

- Deze getallen kan je ook aanduiden op de schets die je maakt.

van rekenvoorbeeld naar onbekende x:
- De stap naar een veranderlijke x is nu niet zo groot meer:
Als je aan de twee kanten x cm afknipt, wordt de zijde = 40 - 2x .
De hoogte = x .
De inhoud = (40 - 2x) . (40 - 2x) . x.
Distributief uitgewerkt vinden we als functievoorschrift voor de inhoud:
I(x) = 4x³ - 160 x² + 1600 x

- Bereken de nulwaarden van deze functie en maak het tekenoverzicht:
D = 25600 met x₁ = 6,67 en x₂ = 20
Als tekenoverzicht vinden we:

x                      6,67            20
I ' (x)       +           0        -       0          +
I (x)         ↗     max ↘   min    ↗

De inhoud zal maximaal zijn, wanneer we 6,67 cm wegsnijden.
opm: Het zinvol domein is niet onbeperkt.
We kunnen nooit minder dan 0 cm wegknippen.
We kunnen nooit meer dan 20cm kunnen wegknippen, want dan knippen we het hele karton weg: 2 . 20 = 40

controle
Je kan op het applet controleren of het wegknippen van 6,67cm inderdaad een maximale inhoud oplevert.

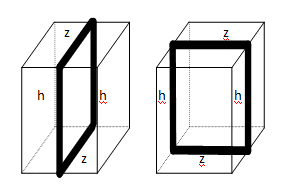
rekenvoorbeeld
om het lint rond de doos te binden, heb je in het totaal 4 keer de hoogte nodig en 4 keer de zijde van het grondvlak.
We vinden: 4z + 4h = 200.

Als we als zijde 10 cm nemen: 200 - 4 . 10 = 160
4h = 160
h = 40
De inhoud van de doos wordt: 10 . 10 . 40 = 4 000cm³

Als we als zijde 20 cm nemen: 200 - 4 . 20 = 120
4h = 120
h = 30
De inhoud van de doos wordt: 20 . 20 . 30 = 12 000cm³

van rekenvoorbeeld naar onbekende x:
Als we als zijde 20 cm nemen, krijgen we: 200 - 4x = 4h
50 - x = h.
De inhoud van de doos wordt x . x. (50 - h)

I ' (x) = - 3x² + 100x
Om de maximale waarde van de inhoud te vinden moet de afgeleide gelijk worden aan 0.
We vinden:
- 3x² + 100x = 0
x . ( -3x + 100) = 0
Oplossingen zijn x = 0 en x = 100/3 = 33,3

I ' (x) = -3x? + 100 - 0 + 0 -
I (x) ↘ min ↗ max ↘

Het zinvol domein = [ 0 , 50 ]
want met een zijde van 50cm is het lint van 2m al op aan de zijden alleen al.

Als oplossing vinden we:
De zijde van de doos = x = 33,3 cm
De hoogte van de doos = 50 - x = 16,7 cm

controle:
de totale lengte die we gebruiken bij het inpakken is 4 . 33,3 + 4 . 16,7 = 200.
Ga nu in het applet na of de gevonden waarden inderdaad een maximale inhoud opleveren.

oplossing stadion
De totale lengte van 400m wordt gevromd met een cirkelomtrek en 2 keer de lengte van de rechthoek.
2π r + 2l = 400
r = (200 - l) / π

We stellen de lengte gelijk aan x.
De breedte van de rechthoek is gelijk aan de straal van de cirkel = (400 - 2x )/ π
De oppervlakte van de rechthoek = x . (400 - 2x )/ π
f(x) = ( -2x² + 400x ) / π heeft een maximum voor x = 100.

oplossing balk
Uit Pythagoras vinden we: b² + h² = 900
Met b = x vinden we h² = 900 - x²
bh² wordt dan x . (900 - x²) = - x³ + 900x.
f(x) = - x³ + 900x heeft een maximum voor x = 17,3cm.

oplossing rondboograam:

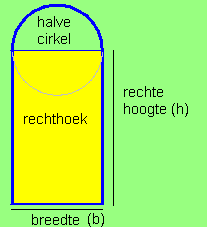De oppervlakte van het rondboograam bestaat uit een halve cirkel en een rechthoek.
De totale oppervlakte van het raam vinden we dus als 1/2.(π . r²) + b . h
We moeten nu de verschillende grootheden r, b en h uitdrukken in 1 veranderlijke x.
Hiervoor gebruiken we de gegeven omtrek van het raam = 90 cm
Deze omtrek wordt gevormd door de som van:
- eenmaal de breedte van het raam = b
- tweemaal de rechte hoogte van het raam = 2 . h
- de halve omtrek van het raam = π . r ( want een cirkelomtrek = 2π . r)

Wat nemen we nu best als x?
De straal van de cirkel is de helft van de breedte van het raam.
Om in de formule van de cirkelomtrek en -oppervlakte de factor 1/2 te vermijden,
kunnen we de straal gelijkstellen aan x. We drukken nu hoogte, breedte en straal uit in x:

straal = x
breedte b = 2x
de hoogte leiden we af uit de totale som van 90 cm: b + 2h + π r wordt dan:
2x + 2h + π. x = 90
2h = 90 - 2x - π .x
h = 45 - x - π/2. x

De oppervlakte van het raam drukken we nu uit in de veranderlijke x
O(x) = 1/2.(π . r²) + b . h
O(x) = 1/2.(π . x²) + 2x . (45 - x - π/2. x)
O(x) = 1/2.(π . x²) + 90x - 2x² - π. x²

Deze oppervlakte is maximaal als de afgeleide gelijk wordt aan 0.
O'(x) = π . x + 90 - 4x - 2π. x = 0
90 + ( π - 4 - 2π ). x = 0
90 + ( - 4 - π ) . x = 0
90 = ( 4 + π ) . x
90 / ( 4 + π ) = x = 12,6

De oppervlakte van het raam wordt maximaal bij volgende afmetingen :
straal r = x = 12,6 cm
breedte b = 2x = 25,2 cm
rechte hoogte h = 45 - x - π/2. x = 45 - 12,6 - π/2. 12,6 = 12,6

We controleren nog of met deze afmetingen de totale omtrek inderdaad 90 cm is:
b + 2h + πr = 12,6 + 2. 12,6 + π .12,6 = 90

oplossing cilinder in kegel
De straal van de kegel = |AD| = 4cm
De hoogte van de kegel = |DE| = 6cm
Wanneer we de straal van de cilinder x noemen,
kunnen we de hoogte uitdrukken in functie van deze straal

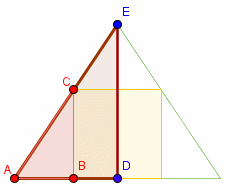De cilinder bepaalt twee gelijkvormige driehoeken: ΔABC en ΔADE.
Hierin vinden we volgende gelijkheid :

h = 1,5. (4 - x)
h = 6 - 1,5x

De inhoud van een cilinder vinden we als I = π r² . h
We krijgen dus:
I (x) = π x² . (6 - 1,5x)
I (x) = 6π x² - 1,5π x³

De inhoud wordt maximaal als I ' (x) = 0
I ' (x) = 12 π x - 4,5 π x² = 0
π x (12 - 4,5 x) = 0

nulpunten zijn x = 0cm en x = 8/3 (2,67)cm.
De inhoud van de cilinder zal maximaal zijn voor een straal van 2,67cm.
De hoogte van de cilinder is dan 6 - 1,5x = 6 - 1,5. 2,67 = 2 cm

\|CB\|	=	\|ED\|
\|AB\|	=	\|AD\|