rekenen met machten wiskunde-interactief.be

                         

machten met hetzelfde grondtal vermenigvuldigen en delen
 



 

 

 

macht van een som - product - quotiënt - macht
 

 De macht van de som ≠ de som van machten.  (a + b) n ≠ an + bn  
 De macht van het product = het product  van machten  (a . b) n = an . bn
 De macht van een quotiënt = het quotiënt van de machten.
 (  a  ) n =   an
b   bn
 De macht van een macht = de macht met het product van de
 exponenten als exponenten		  (am) n = am . n
 In al deze formules zijn a en b reële getallen, verschillend van 0.
 n is een natuurlijk getal.

 

 

 

 

 


 

 

negatieve exponenten

We kennen: We weten ook:   
Hieruit vinden we:       
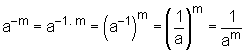 We definiëren:
 a -n =      1  
 an

   Hierin is a een reëel getal, verschillend van 0.
   n is een natuurlijk getal, verschillend van 0.

Met deze uitbreiding naar negatieve machten kunnen we rekenregels voor machten veralgemenen.
De rekenregels voor natuurlijke exponenten gelden bij uitbreiding ook voor gehele exponenten.

 

 

 

 

 

 

 

 

 

a0
Met de definitie voor negatieve exponenten kunnen we duidelijk illustreren waarom we a0 definieerden als1
Als we de tabel volgen van links naar rechts merk je dat we telkens delen door a:

a3

a2

a1

a0

a-1

a-2

a-3

a . a . a

a . a

a

1

1/a

1/(a . a)

1/(a . a . a)

 

 

 

overzicht machten met gehele exponenten:

an = a . a ... a   (n factoren)                    

(a + b) n ≠ an + bn                                   

 (a . b) n = an . bn                                     

(  a  ) n = an                                                  
b   bn

(am) n = am . n                                         

a-n =      1                                                   
 an

a0 = 1

(am) n = am . n                                       

In deze formules zijn a en b reële getallen, verschillend van 0.
m en n zijn gehele getallen, verschillend van 0.

 

 

teken van een macht
Is b.v. (- 2)198 positief of negatief?
De macht is een product van 198 factoren.

We kunnen dus het teken afleiden uit de tekenregel voor het product van getallen:
even exponenten:   oneven exponenten:
22 = 2 . 2 = 4      
(-2)2 = (-2) . (-2) = 4

Zo ook:
24 = (-2)4 = 16

het resultaat is steeds positief		              23 = 2 . 2 . 2 = 8       
(-2)3 = (-2) . (-2) . (-2) = - 8

Zo ook:
25 = 32  
maar (-2)5 = -32
het teken hangt af van het teken van het grondtal

Algemeen:

 - Een macht an met een even exponent n is steeds positief.

 - Een macht an met een oneven exponent n heeft hetzelfde teken als het grondtal a.   

   Hierin is a een reëel getal, verschillend van 0.
   n is een natuurlijk getal, verschillend van 0.

Let op: 
minteken voor de macht:   - 24 = - ( 24) = - 16        terwijl  (- 2)4 = 16
twee mintekens:
  - ( - 2)4 = - (16) = - 16  
  - ( - 2)3 = - (-8) = 8  
  Twee mintekens heffen elkaar niet zomaar op!
  Reken steeds stap voor stap en werk eerst de haakjes uit.

- negatieve exponent: 2-3 =     1    =  1      de negatieve exponent bepaalt wel de uitkomst, maar niet het teken.            
 23  8


 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

naar startpagina
 naar sitemap
 het begrip macht
 wetensch.schrijfwijze

hetzelfde grondtal
 rekenen met machten
 negatieve machten
 a0
 overzicht
teken van een macht

oefeningen