normale verdeling
wiskunde-interactief.be
de normale
kromme:
N(μ,σ)
Histogrammen vertonen vaak een symmetrische, klokvormige
verdeling,
die we goed kunnen benaderen door een vloeiende kromme. We noemen ze
dichtheidskrommen.
Vaak stellen we bij deze krommen vast:
- ze zijn symmetrisch ten
opzichte van een verticale door het gemiddelde
- de meeste waarden liggen in de buurt van het gemiddelde
- hoe verder weg van het gemiddelde, hoe minder waarden |
Zulke krommen noemen we normale krommen.
Carl Friedrich Gauss onderzocht het verloop. We noemen ze daarom ook
gausscurve.
Hij vond ook het voorschrift:
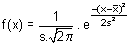
We noteren deze verdeling als
Norm (μ,σ)
met:
μ
als het gemiddelde van de
verdeling
σ
(= s) als standaardafwijking
|
normaal
verdeelde gegevens |
|
Als een histogram goed overeenkomt met de
normale kromme,
zeggen we dat de gegevens normaal verdeeld zijn.
- het gemiddelde van de gegevens komt dan overeen met
μ,
- de standaardafwijking s van de gegevens met
σ
Maak in het applet de ondergrens a kleiner en bovengrens b groter,
telkens met een veelvoud van
σ
|
We
merken:
- 68% van de gegevens ligt niet verder dan
σ
van het gemiddelde
- 95% van de gegevens ligt niet verder dan 2σ
van het gemiddelde
- 99% van de gegevens ligt niet verder dan 3σ
van het gemiddelde
De grootte van de
standaardafwijking speelt hierbij geen rol.
|
|
Standaardnormale verdeling Norm(0,1) :
z-waarden
We kunnen uitdrukken
hoeveel standaardafwijkingen een waarde afwijkt van het gemiddelde.
Dit noemt men de z-waarde.
Het is met deze waarde dat je berekent hoeveel procent van de gegevens zich
beneden een waarde bevinden.
(computers en rekenapparaatjes doen dit in jouw plaats)
Deze aflezingen kan je ook doen in het onderstaande applet.
Hoeveel % van de gegevens is
kleiner dan?
Hoeveel % van de gegevens is kleiner dan... (of groter dan)?
Deze vraag kunnen we nu ook beantwoorden voor elke willekeurige
verzameling normaal verdeelde gegevens.
Computer of rekenapparaat maken voor jou de omrekening naar z-scores.
In het applet kan je gemiddelde, standaardafwijking en waarde aanpassen.
|
Hoeveel % van de gegevens ligt tussen...
Hoeveel % is kleiner dan een gegeven bovenwaarde?
Hoeveel % is kleiner dan een gegeven onderwaarde?
Het verschil van beide zegt ons hoeveel % binnen een bepaald interval ligt.
In het applet kan je onder- en bovenwaarde maar ook gemiddelde en
standaardafwijking aanpassen.
Hoe groot is de waarde...
Hoe groot moet een waarde zijn als je wil dat 70 % van de gegevens kleiner
is dan deze waarde?
Dit bereken je met het commando InversNormaal[
<Gemiddelde>, <Standaardafwijking>, <Waarschijnlijkheid> ]
![]()