afgeleiden - overzicht

differentiequotiënt

 

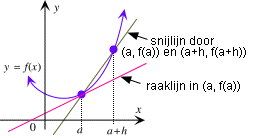
 Gemiddelde verandering van f(x) over [a, b]:
 Differentiequotiënt

 De gemiddelde verandering van f(x) over het interval [a, b] is

    gemiddelde verandering =
    f

    x
    		 =
    f(b) - f(a)

    b - a
    		.
 We noemen deze gemiddelde verandering ook het
 differentiequotiënt van f(x) over het interval [a, b].
 Gemiddelde verandering van f(x) over [a, a+h]
 (We vervangen b door a+h.) 
 De gemiddelde verandering van f(x) over het interval [a, a+h] is
    gemiddelde verandering =
    f(a+h) - f(a)

    h
    		 .

 Voorbeeld:

 f(x) = 2x2 - 4x + 1.
 Bereken de gemiddelde verandering van f(x) over het interval [2, 4].

    Differentiequotiënt  =
    f(4) - f(2)

    4 - 2
    =
    17 - 1

    2
    		 =8.
 

 

 

 

 

 

 

 

afgeleide

 

 Ogenblikkelijke verandering van f(x) voor x = a:
 Afgeleide

 De ogenblikkelijke verandering van f(x) voor x = a vinden we door h
 (= de breedte van het interval [a, a+h] ) naar 0 te laten naderen.
 We  krijgen dan de limietuitdrukking:
ogenblikkelijke verandering =
lim
h0
f(a+h) - f(a)

h
 .
 We noemen deze  ogenblikkelijke verandering de afgeleide van f(x) 
 voor x = a, en noteren ze als f '(a) (

    f '(a)=
    lim
    h0
    f(a+h) - f(a)

    h
    		 .
 Voorbeeld
 f(x) = 2x2 - 4x + 1. Wat is de afgeleide van f(x) voor x = 2 ?
 

 

 

 

 

 

 

 

 

benadering van de afgeleide

 

 Benadering van de afgeleide

 We kunnen f '(a) benaderen door een tabel met steeds kleinere waarden
 voor h en het bijhorend quotiënt:

    f(a+h) - f(a)

    h

 

 

 

 


 Een snelle benadering
 We kunnen ook een zeer kleine waarde van h nemen en aannemen
 dat dit  een goede benadering is:

    f'(a)
    f(a+0.0001) - f(a)

    0.0001
    		 .
 Voorbeeld
 f(x) = 2x2 - 4x + 1. We benaderen f '(2).
 Het differentiequotiënt (voor a = 2) is
f(2+h) - f(2)

h
=
2(2+h)2-4(2+h)+1 - (2(2)2-4(2)+1)

h
 We nemen steeds kleinere waarden voor h:
 
h 10.1 0.010.001 0.0001
Differentiequotiënt 64.2 4.024.002 4.0002

 De waarden naderen 4. We besluiten hieruit: f '(2) 4.

 Een snelle benadering
 We nemen 0.0001 als waarde voor h:

    f'(2)
    f(2+0.0001) - f(2)

    0.0001
    =
    f(2.0001) - f(2)

    0.0001
    =
    1.00040002 - 1

    0.0001
    		 =4.0002.
 

 

 

 

 

 

 

benadering van de afgeleide

 

 Benadering van de afgeleide

 We kunnen f '(a) benaderen door een tabel met steeds kleinere waarden
 voor h en het bijhorend quotiënt:

    f(a+h) - f(a)

    h

 

 

 

 


 Een snelle benadering
 We kunnen ook een zeer kleine waarde van h nemen en aannemen
 dat dit een goede benadering is:

    f'(a)
    f(a+0.0001) - f(a)

    0.0001
    		 .
 Voorbeeld
 f(x) = 2x2 - 4x + 1. We benaderen f '(2). 
 Het differentiequotiënt (voor a = 2) is
f(2+h) - f(2)

h
=
2(2+h)2-4(2+h)+1 - (2(2)2-4(2)+1)

h
 We nemen steeds kleinere waarden voor h:
 
h 10.1 0.010.001 0.0001
Differentiequotiënt 64.2 4.024.002 4.0002

 De waarden naderen 4. We besluiten hieruit: f '(2) 4.

 Een snelle benadering

    f'(2)
    f(2+0.0001) - f(2)

    0.0001
    =
    f(2.0001) - f(2)

    0.0001
    =
    1.00040002 - 1

    0.0001
    		 =4.0002.
 

 

 

 

 

 

 

afgeleide als helling

 

 Afgeleide als helling: Meetkundige benadering

 De helling van de snijlijn door de grafiekpunten van f voor x = a
 en x = a+h  vinden we met het differentiequotiënt:

    helling snijlijn= differentiequotiënt
    =
    f(a+h) - f(a)

    h
    		.
 De helling van de raaklijn door het grafiekpunt van f voor
 x = a is gelijk aan de afgeleide f '(a).
    helling raaklijn= f'(a)
    =
    lim
    h0
    f(a+h) - f(a)

    h
    		.

 
 

 

 

 

 

 

 

berekenen

 

Berekenen van de afgeleide met de definitieformule

We kunnen de afgeleide berekenen met de definitie:

  1. Schrijf de definitie van afgeleide:
    f'(x)=
    lim
    h0
    f(x+h) - f(x)

    h
    		 .
  2. Vervang de functiewaarden voor f(x+h) en f(x)
    We kunnen deze afgeleide berekenen voor een welbepaalde waarde, of algemeen voor de veranderlijke x.
  3. Werk de teller uit en bereken de limietuitdrukking.
Voorbeeld

f(x) = 2x2 - 4x + 1.  We berekenen f '(x) met de definitieformule van afgeleide:

f'(x)=
lim
h0
f(x+h) - f(x)

h
=
lim
h0
(2(x+h)2-4(x+h)+1) - (2x2-4x+1)

h
=
lim
h0
2x2+4xh+2h2-4x-4h+1-2x2+4x-1

h
=
lim
h0
4xh+2h2-4h

h
=
lim
h0
h(4x+2h-4)

h
=
lim
h0
 (4x+2h-4)
=4x-4

Dus, f '(x) = 4x-4.

 

 

 
 
 
 

naar startpagina  differentiequotiënt    afgeleide    benadering    afgeleide als helling    berekening 

verder ook: afgeleide functie overzicht       oefeningen  opgeloste oefeningen