oppervlakte

 

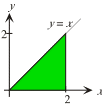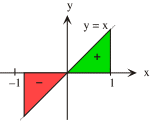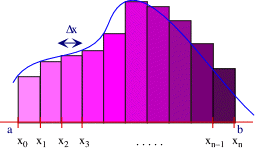
Integralen en oppervlakte De oppervlakte tussen de x-as en de grafiek benaderen we door de som van rechthoekjes. Door de rechthoekjes smaller te nemen, verbeteren we de benadering. hoofdstelling: de afgeleide van de oppervlakte onder de grafiek van een functie f is gelijk aan de functie f zelf. We kunnen de oppervlakte tussen grafiek en x-as berekenen door de omgekeerde bewerking van "bereken de afgeleide van".

primitieve functie

 

Primitieve functies Een primitieve functie van een functie f is een functie F, zo dat F ' = f. In woorden: een primitieve functie van een gegeven functie is een functie waarvan de afgeleide de gegeven functie is.

Voorbeelden 1.  Een primitieve functie van 4x3 is x4     Want de afgeleide van x4 is 4x3 2.  Een andere primitieve functie van 4x3 is x4 + 7     Want de afgeleide van x4 + 7 is 4x3 3.  Nog een primitieve functie van 4x3 is x4 - 2     Want de afgeleide van x4 - 2 is 4x3 Een functie heeft nooit slechts één primitieve functie. Daarom schrijven we steeds een constante c.

machtsregel

 

Machtsregel voor primitieve functies De prim.functie van xn dx = xn+1 /(n + 1) + c     met n ≠ -1 De prim.functie van x-1 dx = ln |x| + C In Woorden: Om de primitieve functie te vinden van  xn, verhogen we de exponent met één, en delen we door deze nieuwe exponent. Deze regel werkt op voorwaarde dat n verschillend is van -1.

Voorbeelden     f (x)   F (x) 1.   x2   x3 /3 + c 2.   1/x4 =  x-4   - x-3 /3 + c 3. 1 = x0   x1 /1 + c = x + c

som en product

 

Rekenregels voor primitieve functies (a) Somregel primitieve functie van [f(x) ± g(x)] dx = F(x) dx ± G(x) dx In woorden:De primitieve functie van een som van twee functies is gelijk aan de som van de integralen van deze functies. (b) Vermenigvuldiging met een constante primitieve functie van k f(x) dx = k . F(x) dx In woorden: De primitieve functie van een functie, vermenigvuldigd met een constante is gelijk aan die constante, vermenigvuldigd met deze constante.  (M.a.w.: We mogen een constante buiten het integraalteken plaatsen)

Voorbeelden   f (x)   F (x) 1.   x3+1   x4 /4 + x + c 2. 6x2 + 4   6x3 /3 + 4x + c = 2x3 + 4x + c

bepaalde integraal

 

Bepaalde integraal en oppervlakte De oppervlakte tussen de x-as en de grafiek van de functie f met x als veranderlijke over het interval  [a, b], noteren we als b     a f(x) dx Integraal en teken Voor de intervallen waar de functiewaarden negatief zijn, levert de integraal een negatief resultaat op. De totale oppervlakte in onderstaande figuur berekenen we dus als twee integralen. (integraal van a tot het nulpunt) - (integraal van het nulpunt tot b). Zonder rekening te houden met het teken wordt de integraal over [a, b] = 0

Voorbeelden 1. 2     0 x dx = 2 Totale oppervlakte = 2               2. 1     -1 x dx = 0 Rood + Groen = 0

berekenen

 

Berekenen van bepaalde integraal: Als F een primitieve functie is van een functie f, continu en bepaald in het interval [a, b], dan bereken we de bepaalde integraal als volgt: b     a f(x) dx = F(b) - F(a). In woorden: Om de bepaalde integraal te berekenen, bepalen we de primitieve functie F van de functie f, we vullen hierin de intervalgrenzen in, en maken het verschil van beide functiewaarden: F(bovengrens) - F(ondergrens).

Voorbeeld 1 Daar F(x) = x2 de primitieve functie is van f(x) = 2x, 1     0 2x dx   =   F(1) - F(0) = 12 - 02 = 1. Voorbeeld 2 1     -1 (1-x2) dx = x - x3/3 1     -1 = 2 3 - (- 2 3 ) = 4 3

substitutiemethode

 

Integratie door substitutie Soms kunnen we een integraal oplossen door substitutie. we stellen een vorm in de veranderlijke x gelijk aan een nieuwe veranderlijke u.  f dx = g du Methode 1. Schrijf u als een functie van x. 2. Bepaal de afgeleide en  bepaal ook de verhouding dx t.o.v. du. 3. Vervang elke vorm in x door de overeenkomende vorm in u. Bepalen van u Er is geen vaste methode of 'snelle regel die altijd werkt'. Kijk naar volgende mogelijkheden: Stel u gelijk aan een uitdrukking die verheven wordt tot een macht. Stel u gelijk aan een uitdrukking waarvan de afgeleide voorkomt als een factor in de integraal.  Stel u gelijk aan de noemer van een rationale vorm. Als de variabele x niet kan geëlimineerd worden door de substitutie, probeer dan een andere substitutie (of een andere methode...)

Voorbeeld   (x2+1)(x3 + 3x - 2)2 dx   u =  x3 + 3x - 2   Bepaal u du =  3x2 + 3 dx Leid af: du =  3(x2 + 1) dx  Schrijf zo dat je elke vorm met x kan vervangen  du 3 = (x2 + 1)dx      Vervang nu de vormen met x door overeenkomende vormen met u: (x2+1)(x3 + 3x - 2)2 dx = u2 du 3 Vervang de vormen in x = 1 3 u2 du Breng de constante buiten = 1 3 u3 3 + C Bepaal de primitieve functie = (x3+3x-2)3 9 + C Schrijf nu alles terug in x