De afgeleide van f(x) = sin x vinden we met de formule:

dx
=
cos x.
|
afgeleiden van goniometrische functies |
|
|
Andere formules kunnen we afleiden van deze formule.
De
afleiding van deze formule vind je onderraan.
Oefening 1: Bereken de afgeleiden van:
a) f(x) = x sin x
Met de productregel vinden we:
| f ' (x) | = | (1)(sin x) + (x)(cos x) = sin x + x cos x |
b) f(x) = cosec x
| f(x) = cosec x = |  sin x | . |
Met de quotiŽntregel vinden we:
| = |
|
|||
| = |
|
| c) f(x) = |  sinx | , |
Met de quotiŽntregel vinden we:
 dx | = |  (x2+x)(cos x) (x2+x)(cos x) sin2x | , |
d) y = sin(3x2 1)
1)
Dit is een samengestelde functie. We leiden deze af met de regel:
 dx | sin u = cos u |  dx |
zodat:
 dx |
sin (3x2 1) 1) |
= |
|
= | 6x cos(3x2 1) 1) |
|
We schrijven de factor 6x vooraan om
verwarring te vermijden wanneer we schrijven cos(3x2 |
Bedoelen we cos[(3x2 1)(6x)]
of [cos(3x2 1)(6x)]
of [cos(3x2 1)](6x)? 1)](6x)? |
|
De afgeleide van f(x) = cos x vinden we met de formule:
|
We leiden deze formule af vanuit de goniometrische gelijkheid cos x = sin(p/2 x)
x)
f(x) = cos x = sin(p/2 x),
x),
Dit is een samengestelde functie. We krijgen:
| = |
|
||||
| = |
|
(want p/2 is
een constante, en d/dx( x) = x) =  1) 1) |
|||
| = |  sin x sin x |
(want cos(p/2 x) = sin x) x) = sin x) |
andere
goniometrische functies
De andere goniometrische functies kunnen uitgedrukt worden met sinus en cosinus.
Met de 2 formules voor cosinus en sinus kunnen we dus ook de andere formules
afleiden.
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
Oefening 2: Bereken de afgeleiden van:
a) f(x) = tan(x2 1)
1)
Dit is een samengestelde functie. We vinden:
 dx |
tan u = sec2u |  dx |
 dx |
tan(x2 1) 1)
| = | sec2(x2 1) 1) |
 1) 1) dx |
|
| = | 2x sec2(x2 1). 1). |
||||
b) f(x) = cosec(e3x)
cosec u =  cosec
u cotan u cosec
u cotan u |
 dx |
 dx |
cosec(e3x) | = |  cosec(e3x) cotan(e3x) cosec(e3x) cotan(e3x) |
 dx |
|
| = |  3e3x cosec(e3x) cotan(e3x). 3e3x cosec(e3x) cotan(e3x). |
(de afgeleide van e3x is 3e3x) | |||
c) f(x) = e xsin(2x)
xsin(2x)
We gebruiken de productregel:
| f '(x) | = |
|
|||||
| = |
|
(want d/dx sin u = cos u du/dx) | |||||
| = |  e e xsin(2x) + 2e xsin(2x) + 2e xcos(2x). xcos(2x). |
d) f(x) = sin2x
sin2x = (sin x)2.
f(x) is het kwadraat van de sinusfunctie en dus een samengestelde functie. We
vinden:
 dx |
[u2] | = | 2u |  dx |
 dx |
[(sin x)2] | = | 2(sin x) |  dx |
= | 2 sin x cos x. |
e) f(x) = sin(x2)
Dit is een samengestelde functie. We vinden:
 dx |
sin u = cos u |  dx |
 dx |
sin(x2) | = | cos(x2) |  dx |
| = | 2x cos(x2). | |||
Formule voor de afgeleide functie van f(x) = sin x
 dx |
sin x | = | cos x. |
| f ' (x) = | h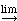 0 0 |
 f(x) f(x) h |
Voor f(x) = sin x kunnen we dus schrijven:
 d |
sin(x) = |
h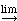 0 0 |
 sin(x) sin(x) h |
. . . . (I) |
In de teller staat sin(x+h). Hiervoor kennen we de
formule sin(x+h) = sin x cos h + cos x sin h.
We vullen deze formule in de teller in:
 d |
sin(x) = |
h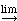 0 0 |
 sin(x) sin(x) h |
. |
Uit de eerste en derde term plaatsen we sin x buiten haakjes
 d |
sin(x) | = |
|
|||||||
| = |
|
|||||||||
| = |
|
We krijgen nu de som van twee limieten.
| De eerste limiet wordt: | h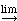 0 0 |
 1) 1)  h |
= | 0 |
| De tweede limiet wordt | h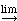 0 0 |
sin h |
= | 1 |
Zodat uiteindelijk:
 dx |
sin x = sin x (0) + cos x (1) = cos x. |
|
afgeleide van sinus |