algebra van Boole wiskunde-interactief.be
George Boole (1815-1864)
George
Boole werd geboren in Lincoln, Engeland, als zoon van een
Zoek je een schilderij van Rubens, maar geen landschap, dan kan je dat
bijvoorbeeld bij Altavista
met een 'advanced search'. Hier gebruik je de zogenaamde Booleaanse operatoren
AND, OR, NOT
Ook Google kent geavanceerd zoeken. De Booleaanse operatoren worden hier omschreven:
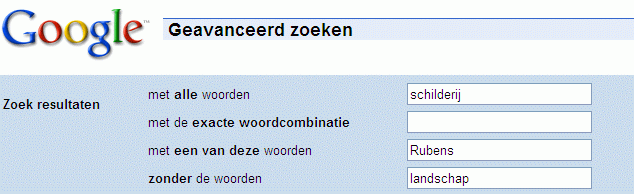
EN, OF en NIET kennen we al uit de verzamelingenleer.
We passen ze toe op volgende verzamelingen:
U = verzameling van alle lln van de school
A = verzameling van alle meisjes van de school
B = verzameling van alle zesdejaars
 |
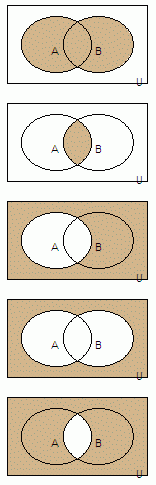A È B |
bevat: alle llln die meisje zijn of in
het zesde jaar zitten voorwaarde: behoort tot A OF tot B (of tot beide) |
| A Ç B | bevat: alle meisjes uit de
zesde jaren voorwaarde: behoort tot A EN tot B |
|
| A | bevat: alle jongens van de school
voorwaarde: behoort NIET tot A |
|
| A È B | bevat: alle jongens die niet in het
zesde jaar zitten voorwaarde: behoort NIET tot A EN NIET tot B |
|
| A Ç B | bevat: iedereen, behalve de meisjes die
in het zesde jaar zitten voorwaarde: behoort NIET tot A OF NIET tot B |
| Het uitwerken van deze laatste twee eigenschappen is niet evident: | |
| A È B : | een leerling zit hierin als hij geen meisje is, en niet in het
zesde jaar zit we vinden: A È B = A Ç B |
| A Ç B: | een leerling zit hierin als hij geen meisje is ofwel niet in het
zesde jaar zit we vinden: A Ç B = A È B |
| Deze twee eigenschappen noemt men de wetten van De Morgan: |
Het al dan niet tot een verzameling behoren, kunnen we weergeven in een
waarheidstafel.
Voor de bewerkingen met verzamelingen krijgen we:
Unie van verzamelingen:
Doorsnede van verzamelingen:
Complement van een verzameling:
In een niet-ledige verzameling kunnen we volgende drie bewerkingen
definiëren:
som: x + y
product: x . y
complement: x
Een dergelijke structuur noemt men een Boole-algebra als deze bewerkingen voldoen aan volgende axioma's:
|
||||||
|
||||||
|
||||||
|
||||||
algebra van Boole en
verzamelingenleer
De analogie tussen een algebra van Boole en de verzamelingenleer is
duidelijk:
 |
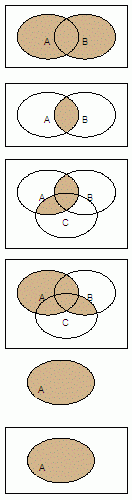Commutatieve
eigenschappen A È B = B È A A Ç B = B Ç A |
Commutatieve
eigenschappen a + b = b + a |
| Distributieve
eigenschappen A Ç ( B È C) = (A Ç B) È (A Ç C) A È ( B Ç C) = (A È B) Ç (A È C) |
Distributieve
eigenschappen a . ( b + c ) = ( a . b ) + ( a . c ) a + ( b . c ) = ( a + b ) . ( a + c ) |
|
| Neutrale elementen A Ç f = A A Ç U = A |
Neutrale elementen a + 0 = a a . 1 = a |
We merken hier ook op:
Met elk optellingsaxioma komt een vermenigvuldigingsaxioma overeen:
verwissel je in een axioma de bewerkingen + en . en de neutrale elementen 0
en 1,
dan bekom je een ander axioma.
Dit noemen we het dualiteitsprincipe.
We kunnen een Boole-algebra beperken tot de neutrale elementen 0 en 1.
Deze beperking vindt een belangrijk toepassingsgebied in digitale schakelingen.
We controleren de voorwaarden voor een Boole-algebra:
- De bewerkingen zijn intern en commutatief:
Optelling:
Vermenigvuldiging:
Complement:
- Elk element heeft een complement, zo dat a +
a = 1 en a .
a = 0
voor 0: 0 + 1 = 1 en 0 . 1 = 0
voor 1: 1+ 0 = 1 en 1 . 0
= 0
- Voor de distributiviteit van . t.o.v. + vinden we:
| a | b | c | b + c | a . (b + c) | a.b | a.c | (a.b) + (a.c) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Wegens het dualiteitsprincipe geldt meteen ook de distributiviteit van + t.o.v. .
eigenschappen in een Boole-algebra
 |
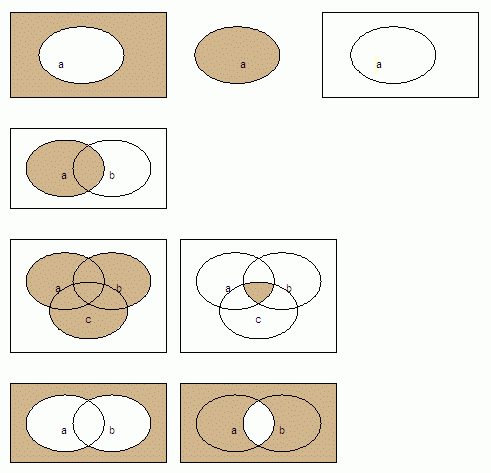1 en 0 noemen we
de opslorpende elementen voor + en 0 |
a + a = a a + 1 = 1 |
|||
| absorptiewetten | a + (a . b) = a
a . (a + b) = a
|
||||
| + en . zijn associatief | (a + b) + c = a + (b + c)
(a . b) . c = a . (b . c)
|
||||
| wetten van de Morgan |
(a + b) =
a .
b (a . b) =
a +
b
|
Door gebruik te maken van deze eigenschappen kunnen we in een Boole-algebra
rekenen. B.v.: