machten_rationale

machten met rationale exponenten wiskunde-interactief.be

We kunnen rekenen met machten:
2² = 2 . 2
2³ = 2 . 2. 2
2ⁿ = 2 . 2 ... 2 (n factoren)

Maar als n negatief is?
Om 2 ^-3 te berekenen kunnen we toch moeilijk -3 factoren nemen?
Wel kennen we aanknopingspunten om machten met negatieve exponenten als 2 ^-3te berekenen.

negatieve exponenten

We kennen: a ^-1 =	1	We weten ook: (a^m)ⁿ = a^{m . n}
	a

Hieruit vinden we: a^-m = a^{-1 . m} = (a^-1)^m = (	1	)^m =	1
	a		a^m

We definiëren:

a^-n =	1
	aⁿ

hierin is a een reëel getal, verschillend van 0
en n een natuurlijk getal, verschillend van 0

We kunnen nu nog een stap verder gaan en ook machten met rationale exponenten definiëren.

rationale exponenten

Uit definitie en eigenschappen van wortels zoeken we hoe we een wortel kunnen schrijven als een macht:

We defini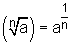ëren:
en

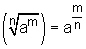
                                                            hierin is a een positief reëel getal
m een geheel getal
en n een natuurlijk getal, verschillend van 0 en 1
(m.a.w. in de exponent schrijven we enkel een minteken in de teller)

eigenschappen

Machten met rationale exponenten volgen dezelfde rekenregels als
machten met gehele exponenten:

a^m . aⁿ = a^m+n
a^m : aⁿ = a^m-n
(a . b)ⁿ = aⁿ . bⁿ(a : b)ⁿ = aⁿ : bⁿ
(a^m)ⁿ = a^m.n

Hierin zijn a en b positieve reële getallen
en m en n rationale getallen.

naar startpagina
rekenen met machten
vierkantswortels
nde machtswortels

begrip nde macht
negatieve exponenten
rationale exponenten
eigenschappen

oef.rat. exponenten