Binomiale verdeling wiskunde-interactief.be                                                                                

Bernoulliverdeling

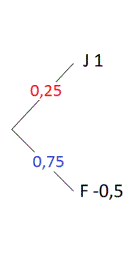
      We nemen als voorbeeld een meerkeuzevraag.
- Je hebt 4 mogelijke antwoorden.
- Bij een juist antwoord krijg je 1 punt.
- Bij een fout antwoord krijg je - 0,5 punten.

Er zijn maar twee mogelijkheden: juist of fout.
De kansverdeling ziet er uit als volgt:

xi                   -0,5                        1                    
P(X=xi)          3/4 (=0,75)         1/4 (=0,25) 

De verwachtingswaarde is:
E(X) = (-0,5) . 0,75  + 1. 0,25 = -0,125
Algemeen:
  Een uniforme kansverdeling heeft heeft precies twee uitkomsten (vaak is dat JUIST of FOUT):      
  Met als kans op JUIST = p, wordt de kansverdeling:      

  xi                   FOUT        JUIST      
  P(X=xi)           q = 1-p       p        

 

 

binomiale verdeling
Kansverdeling
Wanneer eenzelfde Bernoulliverdeling een aantal keer herhaald wordt, spreken we van een binomiale verdeling.
zoals b.v. het 3 keer na elkaar gokken op meerkeuzevragen met 4 mogelijke antwoorden.
Bekijken we even terug de kansboom en de kansverdeling:

  verloop score kans
JJJ
 
JJF
 
JFJ

JFF
 
FJJ

FJF
 
FFJ

FFF		 3
 
1,5
 
1,5

0
 
1,5

0
 
0

-1,5		 0,253
  
0,252 . 0,75
  
0,252 . 0,75
  
0,25 . 0,752
  
0,252 . 0,75
 
0,25 . 0,752
  
0,25 . 0,752
 
0,753
xi -1,5 0 1,5 3
P(X = xi)      1 . 0,753      

= 0,422

 3 . 0,25 . 0,752   

= 0,422

 3 . 0,252 . 0,75  

= 0,141

 1 . 0,253    

= 0,016

Wat is bijvoorbeeld de kans om twee keer juist te antwoorden?

- de kans op JJF is    1 .  1  . 3   =    3    maar ook bij FJJ en JFJ  antwoorden we twee keer juist.
4    4    4        16
- We moeten dus (   1  )2 . (   3  )1  vermenigvuldigen met 3.
4 4
- 3 is het aantal plaatsen waarop de twee juiste antwoorden kunnen staan op 3 mogelijkheden = C  2  = 3 
3

We kunnen het voorbeeld nu verder uitbreiden naar bijvoorbeeld 6 meerkeuzevragen:
De mogelijkheden om 2 juiste antwoorden te hebben zijn nu:
JJFFFF  -  JFJFFF  -  JFFJFF  -  JFFFJF  -  JFFFJ
FJJFFF  -  FJFJFF  -  FJFFJF  -  FJFFFJ
FFJJFF  -  FFJFJF  -  FFJFFJ
FFFJJF  -  FFFJFJ
FFFFJJ

Het aantal mogelijkheden = C  2  = 15 
6
De kans op 2 juiste antwoorden op 6 vragen = C  2  . ( 1  )2 . (  3 )4 = 0,2966
6 4 4

Algemeen:

  Bij een binomiaalverdeling
  - met n deelexperimenten
  - elk met een kans p op succes
 
is de kans op x keer succes op n pogingen =  P( X = x) = C    x  .  px .  (1-p)n-x           
n

Je kan deze berekening uitvoeren op onderstaand applet:

staafdiagram
In een staafdiagram kunnen we voor elke waarde van de stochast de kans uitzetten:

 

Gemiddelde en standaardafwijking
We kunnen ook formules afleiden voor gemiddelde en standaardafwijking:

Een binomiale verdeling van n deelexperimenten, elk met een kans p op succes heeft als
- gemiddelde of verwachtingswaarde E(X) = n . p

- variantie Var(X) = n . p . (1 - p) 
  standaardafwijking  σ = √ Var(X)   

 

Overzicht

  Bij een binomiaalverdeling
  - met n deelexperimenten
  - elk met een kans p op succes
 
  is de kans op x keer succes op n pogingen =  P( X = x) = C  x   .  px . (1-p)n-x                                                       
n

  Hieruit vinden we als kansverdeling:

  xi            0                                    1                                   2                    ...                    n                                
  P(X=xi)
C 0   . p0 (1- p)n        C  1  . p1 . (1 - p)n-1        C  2  . p2 . (1 - p)n-2      ...   C  n  . pn . (1 - p)0          
n n n n

  Het gemiddelde van een binomiale verdeling
  E(X) = n . p          

  De standaardafwijking van een binomiale verdeling
  σ = √ (n . p . (1 - p)

 

galton bord
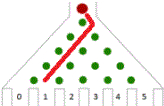
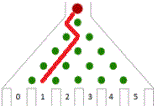
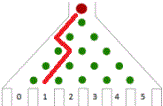
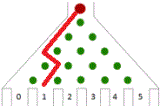
Francis Galton (1822-1911) ontwierp het Bord van Galton of quincunx.

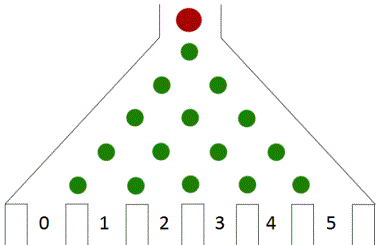Het bord bestaat uit verschillende rijen pinnen.
Het aantal pinnen verhoogt per rij steeds met 1.
Een balletje dat naar beneden valt,
botst eerst op de eerste pin,
hetzij naar links, hetzij naar rechts.
Zo gaat het rij na rij.
De kans dat een balletje naar links of rechts botst, is gelijk,
dus telkens 50% of 1/2.

Wat is nu de kans dat het in een bepaald bakje terechtkomt?
Bekijken we het even theoretisch:
Het balletje belandt onderaan in een bakje na 5 keer botsen op een pin.
Het valt in bakje 1 na als het 1 keer naar rechts valt (en 4 keer naar links).
Die ene keer naar rechts kan de 1e, de 2de ... de 5e pin zijn. Zo zijn er C 1 = 5 mogelijkheden voor bakje 1
5
Met de binomiaalformule berekenen we de kans voor vakje 1
De kans op 1 keer naar rechts vallen op 5 pogingen =  P( X = 1) = C 
1		  
.  (1/2)1 .  (1/2)4  =    		 
5
= 0,156           
5 32

Eenzelfde berekening maken we voor de andere bakjes. De kansverdeling wordt dan:

xi

 0                      1                           2                         3                        4                          5                    

P(X=xi)     1 = 0,03         5 = 0,156         10 = 0,313         10 = 0,313         5 = 0,156         1 = 0,03          
32 32 32 32 32 32
Algemeen:
n rijen pinnen geeft n pogingen
De kans hierbij op k keer naar rechts botsen op n pogingen =  P( X = k) = C 

k

 .  (1/2)n     
n

 

 

 

 

 

 

 

 

 

naar startpagina
 naar sitemap
 telproblemen
 kansverdelingen

Bernoulliverdeling
binomiale verdeling
kansverdeling
 staafdiagram
 gemiddelde en st.afw.
 overzicht
 GRM
toepassing: galton bord