dynamische groei wiskunde-interactief.be 

ongeremde groei
- Een lineaire groei heeft als voorschrift: f(x) = a x + b.
  Hierin staat b voor de beginhoeveelheid, a voor de toename wanneer x met een verhoogt.
  Bij een lineaire groei wordt bij een beginhoeveelheid steeds eenzelfde hoeveelheid bijgevoegd.
  Die aangroei is onafhankelijk van de beginhoeveelheid.

- Een exponentiele groei heeft als voorschrift f(x) = b . a^x.
  Hierin staat b voor de beginhoeveelheid, a voor de groeifactor.
  Deze groeifactor is gelijk aan 1 + i (waarin i staat voor de procentuele aangroei).
  Bij een exponentiele groei wordt een beginhoeveelheid steeds vermenigvuldigd met eenzelfde factor.
  De aangroei is dus wel afhankelijk van de beginhoeveelheid.
  Bij een groeifactor groter dan 1, stijgt de steeds sneller. De groei is ongeremd.

afgeremde groei
Bomen groeien niet tot in de hemel, voorraden aan voedsel, energie of grondstoffen zijn niet oneindig groot.
Een populatie die te groot wordt, zal spontaan afremmen.
Evolueert een populatie naar een stabiele grootte?
En hoe krijgen we deze afremming in een voorschrift?

De Nederlandse wiskundige Ferdinand Verhulst onderzocht dergelijke dynamische systemen.
- Hij vertrok van 1 (=100%) als maximale omvang van een populatie.
- Hij nam een groeifactor aan die afhankelijk is van de grootte van de populatie.
  Bij een ongeremde groei met groeifactor r is x_n+1 = r . x_n.
  Verhulst nam als groeifactor r (1 - x_n)
  Bij een kleine waarde van x_n zal de exponentiele groei nauwelijks of niet worden afgeremd.
  Hoe dichter x_n tot de maximale waarde 1 nadert, hoe kleiner de groei wordt.


grafiek
- We vertrekken van een startwaarde, ergens tussen 0 en1.
- We passen telkens volgende iteratie toe: x_n+1 = x_n . r (1 - x_n)
We spreken van logistische groei en de logistische differentievergelijking.


- De waarden nemen toe.
- De toename is niet meer stijgend, zoals bij een exponentiele groei wel het geval, maar afnemend.
- Na een aantal iteraties evolueren de waarden naar een stabiele waarde.
- Verhoog nu de startwaarde.
  De 'aanloop' verschilt, maar de stabiele eindwaarde blijft dezelfde.
  Die eindwaarde blijft ook ongewijzigd, wanneer je van een waarde vertrekt die hoger is dan de stabiele eindwaarde.
- Verhoog nu de waarde van r.
  De eindwaarde zal nu ook mee verhogen.
  Ze is blijkbaar onafhankelijk van de beginwaarde, maar wordt bepaald door de groeifactor.

- Boven een waarde 2 schiet de populatie eerst even voorbij de eindwaarde, maar schommelt er dan toch naar toe.
- Vanaf een waarde r = 3 gebeurt er echter iets heel eigenaardigs:
  De waarde begint te schommelen tussen twee waarden.
  We kunnen spreken van twee attractoren.
  Deze opsplitsing van de curve noemt men bifurcatie.
- Verhoog de waarde van r nog verder.
  De twee attractoren verwijderen zich verder van elkaar tot ...
  Voor r = 3.45 splitsen beide takken opnieuw.
  Voor nog hogere waarden lijkt de curve te ontaarden in totale chaos.
- Plaats de waarde van de schuifknop r op 4 en verander de beginwaarde.
  Voor enkele beginwaarden verschijnen plots stabiele curves.


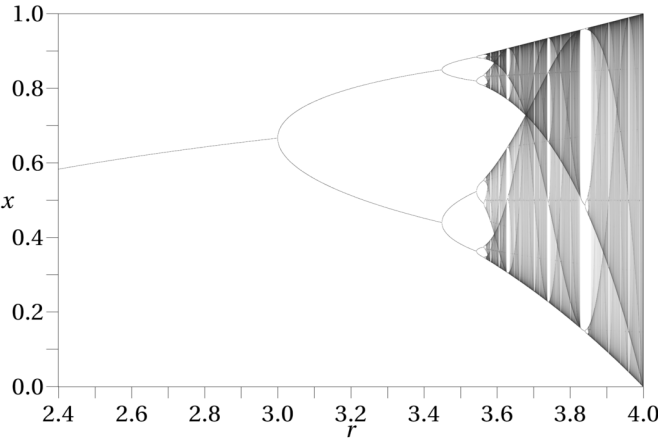
Deze afbeelding illustreert wat er gebeurt voor verschillende waarden van r.
Je ziet de bifurcaties voor r = 3 en r = 3.45.
Het lijkt chaos, maar het is geen willekeur.
In de 'chaos' bij hogere waarden verschijnen opnieuw stabielere vensters, weer met interne bifurcaties.

webgrafiek
Je kunt de groei ook weergeven in een webgrafiek.
- Teken twee grafieken: de grafiek van de functie die de iteratie bepaalt: f(x)= r. x (1 - x) en de rechte y = x.
- Neem een startwaarde op de horizontale as..
- Bepaal het beeld van deze waarde door de functie.
  Dit beeld is het snijpunt van de verticale vanuit de startwaarde met de grafiek van f.
- Deze eindwaarde wordt de nieuwe beginwaarde.
  Teken dus een horizontale lijn door het gevonden snijpunt tot de rechte y=x.
Herhaal dit nu: telkens eerst een verticale tot f, daarna een horizontale tot y = x.

- Blijft r onder 1,1 dan is de groei te klein en evolueren de waarden naar 0.
- Vanaf r = 1,1 naderen de waarden stapsgewijs naar een stabiele waarde.
- Boven r = 2,5 schieten de waarden eerst voorbij de stabiele eindwaarde en draaien er dan in een spiraal naar toe.
- Vanaf r = 3 blijven de waarden ronddraaien in een rechthoek (= 2 attractoren).
- Blijf je r verhogen dan wordt het chaos...



fractaal
Het merkwaardige is dat inzoomen op de figuur gelijkaardige figuur toont als de oorspronkelijke figuur.
Zulke figuur noemen we een fractaal. Kenmerkend voor een fractaal is:
- Een eenvoudige formule levert een complex resultaat op.
- Dit resultaat is niet willekeurig maar zelfgelijkvormig.
  Inzoomen op details levert een gelijkaardige figuur op als het origineel.

Merkwaardig is dat een dergelijk dynamisch groeipatroon opduikt in totaal verschillende sectoren als
economie en biologie.
Meer over fractalen vind je op de pagina fractalen en de pagina complexe iteratie.


Voor wie al wat weet over de Mandelbrot-verzameling, Julia-verzamelingen en attractoren nog dit:
De figuur met r-waarden schaalt perfect met de Mandelbrot-verzameling:
- Ter hoogte van het hartvormige centrale deel is er één attractor, de stabiele eindwaarde.
- Tussen de uiteinden van de tweede grotere bol links daarvan vind je twee attractoren.
- Verder wordt de figuur chaotischer, maar hier en daar duiken stabiele vensters op.
  Die komen overeen met verdikkingen op de reele as van de Mandelbrot-verzameling.
  Bij uitvergroting zie je steeds opnieuw de basisvorm verschijnen.