fractalen wiskunde-interactief.be

Dimensies

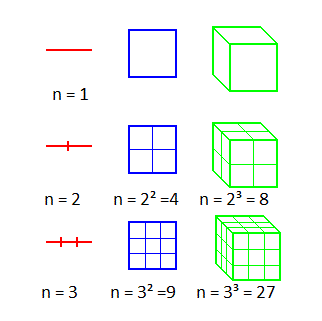
Neem een lijnstuk met lengte 1.
Vergroot je het met factor 2 dan verkrijg je een lijnstuk waar het oorspronkelijke lijnstuk 2¹ keer in past.
Vergroot je het met factor 3 dan verkrijg je een lijnstuk waar het oorspronkelijke lijnstuk 3¹ keer in past. 
We zeggen: de dimensie van een lijnstuk is 1.

Neem een vierkant met zijde 1.
Vergroot je het met factor 2 dan verkrijg je een vierkant waar het oorspronkelijke vierkant 2² keer in past.
Vergroot je het met factor 3 dan verkrijg je een vierkant waar het oorspronkelijke vierkant 3² keer in past. 
We zeggen: de dimensie van een vierkant is 2.

Neem een kubus met ribbe 1.
Vergroot je het met factor 2 dan verkrijg je een kubus waar de oorspronkelijke kubus 2³ keer in past.
Vergroot je het met factor 3 dan verkrijg je een kubus waar de oorspronkelijke kubus 3³ keer in past. 
We zeggen: de dimensie van een kubus is 3.





Fractalen en fractale dimensie
Benoit Mandelbrot boog zich over de vraag: "Hoe lang is de kust van Groot-Brittanie?"
Een simpele vraag, lijkt het, dat kon hij toch gewoon in elke atlas of naslagwerk terugvinden.
Het eigenaardige was dat de afmetingen die hij terugvond, heel erg verschilden.
Mandelbrot ontdekte dat de gevonden lengte afhangt van je meeteenheid.
Of je een paal van 1m in centimeter of in decimeter meet, hij zal altijd even lang zijn, maar bij de lengte van
de kust ging dat niet langer op.

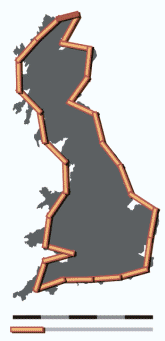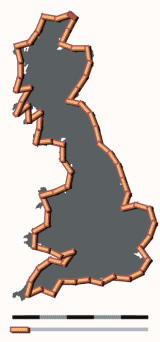11,5 x 200 = 2300 km	28 x 100 = 2800 km	70 x 50 = 3500 km

Neem je een meetlat van 200 km, dan kan je heel moeilijk de onregelmatigheden volgen van de kust.
Met een meetlat van 100 km kan dat al beter, met een van 50 km nog beter.
Het lijkt alsof de kustlijn steeds langer wordt.
Je zou denken dat je de 'juiste' lengte steeds beter benadert door je meetlat te verfijnen, maar de lengte
blijft integendeel onbeperkt toenemen. Ze lijkt oneindig lang, al is ze beperkt.
Mandelbrot besloot dat de kustlijn een dimensie moest hebben tussen 1 en 2.
Eigenaardig is dat bij herhaaldelijk inzoomen de verhouding tussen de gemeten lengte en de zoomfactor
steeds constant bleef: 1,25. Deze verhouding noemde hij de fractale dimensie van de kustlijn.

Deze dimensie is een maat voor de grilligheid van de kust.
Zo bekomt men voor de grillige Ierse westkust 1,26 tegenover slechts 1,10 voor de zachtere oostkust.
De Noorse kust met zijn diepe fjorden komt zelfs uit op 1,52.

Vanuit deze manier van kijken ontstond een nieuw meetkundig begrip: een fractaal.

 


Meetkundige iteraties en hun fractale dimensie

- Verdeel een lijnstuk met lengte l₀=1 in 3 gelijke delen.
- Teken op het middelste deel een gelijkzijdige driehoek.
- Laat het middelste deel weg.
- Herhaal nu de verdeling voor elk lijnstukje van de nieuwe figuur.

lengte1 = 1 lengte2 = 4 . 1/3 = 4/3     lengte3 = 16 . 1/9 = 16/6    lengte3 = 4/3 . lengte2 lengte4 = 64 . 1/27 = 64/27    lengte4 = 4/3 . lengte3

De fractale dimensie bereken je als een breuk.
Het resultaat noemt men ook de Hausdorffdimensie.

De sneeuwvlok van Koch
Pas je bovenstaande iteratie toe op de drie zijden van een gelijkzijdige driehoek,
dan krijg je de sneeuwvlok van Koch.






De driehoek van Sierpinski
- Vertrek opnieuw van een gelijkzijdige driehoek maar verdeel elke zijde nu in 2.
- Teken nu gelijkzijdige driehoeken door deze middens te verbinden.
Je verkrijgt nu 3 driehoeken i.p.v. 1 (de open omgekeerde driehoek telt niet mee), terwijl de zoomfactor 2 is.

De fractale dimensie  van de driehoek van Sierpinski  =	log 3	= 1,585
	log 2

Het tapijt van Sierpinski
- Verdeel een vierkant in 9 gelijke vierkanten door elke zijde in drie te verdelen.
- Haal het middelste vierkant weg.
Je verkrijgt nu 8 vierkanten i.p.v. 1 terwijl de zoomfactor 3 is.

De fractale dimensie  van het tapijt van Sierpinski  =	log 8	= 1,8928
	log 3

Vertrek je van een kubus en werkje de iteratie ruimtelijk uit, dan krijg je de spons van Menger.
Door de verdeling wordt een kubus onderverdeeld in 27 kleinere kubusjes.
Je maakt gaten in de kubus door kubussen weg te halen: het kubusje in het midden van de grote kubus
en telkens de middelste kubusjes van de 6 zijvlakken.
Na het wegnemen hou je dus nog 20 kubusjes over terwijl de zoomfactor 3 is.

De fractale dimensie  van de spons van Menger  =	log 20	= 2,7268
	log 3

De Peano-kurve

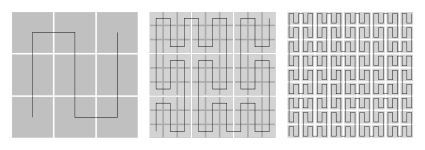
- Verdeel een vierkant in 9 gelijke vierkanten.
- Verbind de middens van de vierkanten door een S-vormige lijn.
Herhaal de iteratie van verdelen en verbinden.
Het resultaat is de Peano-curve.


De S-vormige lijn verschijnt na iteratie 9 keer, terwijl de zoomfactor 3 is.

De fractale dimensie  van de spons van Peano-curve  =	log 9	= 2
	log 3

Een fractale dimensie van 2 betekent ook dat de curve vlakvullend is.
Terwijl de sneeuwvlok van Koch de oorspronkelijke driehoek altijd maar uitbreidt,
kleurt de Peano-curve de tussenliggende ruimte van het vierkant in.





De Pythagorasboom
De Nederlandse wiskundeleraar Albert E. Bosman bedacht in 1942 De boom van Pythagoras:

De bouw van de boom van Pythagoras begint met een vierkant.
Op dit vierkant zet je twee kleinere vierkanten onder een hoek van 45 graden.
Dit herhaal je, en nog eens, en nog eens...

Ook de Pythagorasboom heeft als dimensie 2.

 

 

Mens en natuur
Mandelbrot leerde dat schilders als Cézanne en Picasso ongelijk hadden.
Bomen zijn geen kegels, wolken geen bollen...
Hun onregelmatigheid is juist hun wezenskenmerk.
De mens en natuur zitten vol fractale vormen en structuren.
Het is ook niet moeilijk om dergelijke, schijnbaar complexe vormen te maken.
Slechts een eenvoudige iteratie volstaat en daar is leven nu net goed in: het herhalen van een programma.
 
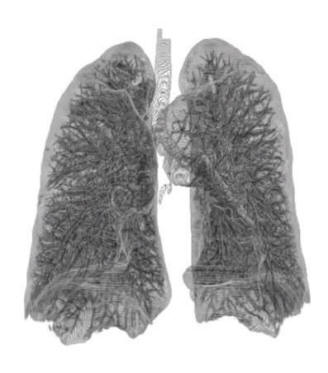
Bloemkolen zijn fractalen, dat is niet moeilijk om te zien, maar ook het bladerdak van een boom is een fractaal.
Deze vorm zorgt voor een maximale bladeroppervlakte, zodat een maximale hoeveelheid licht opgevangen wordt.
Onze longen ons bloedvatenstelsel zijn fractaal voor een maximale opname van zuurstof en doorstroming van bloed.
Schijnbaar ingewikkeld wordt eenvoudig, gewoon door een andere manier van kijken.

Wetenschap en amusement
Fractalen drongen ook door tot het wetenschappelijk onderzoek.
Hoe gedraagt een bepaalt type bandenprofiel zich op een bepaald wegdek?
Geen enkel wegdek is perfect glad. Elk heeft zijn typische onregelmatigheid, precies... het is fractaal.
Door een wegdek als een fractaal te definieren, hoeft men niet met elk bandentype heel de wereld door om het
op testcircuits of gewone wegen uit te proberen.
Bandenprofiel en een fractaal wegdek zijn in een oofwenk aangepast op een computer...

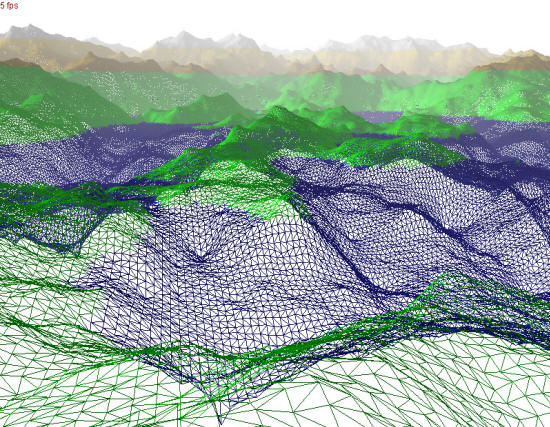
Special effects van science fiction- en fantasyfilms of computergames worden vaak met fractalen gegenereerd.
Exotische planeten, zonnestelsels en fantastische landschappen ontstaan op een computerscherm.
Stap na stap worden lijntjes omgetoverd tot 'echter dan echt'.