logaritmen wiskunde-interactief.be
We kunnen twee getallen bij elkaar optellen en verkrijgen als
resultaat de som: 2 + 3 = 5
Kunnen we ook bewerkingen vormen met de getallen 2, 3 en 5 die als resultaat 2
of 3 hebben?
| a log x = y betekent dat ay = x |
Opmerkingen
1.
we definiëren a log x enkel voor positieve
reële grondtallen a, verschillend van 0 en 1.
(een macht van 0 is steeds gelijk aan 0, een
macht van 1 is altijd gelijk aan 1)
2.
10log x is noemen we de
10-logaritme of
Briggse logaritme van x, we noteren deze ook gewoon als
log x.
3.
elog x noemen we de
natuurlijke logaritme
van x, we noteren deze ook als ln x.
(het getal e
= 2,71828 wordt verder gedefinieerd op de pagina exponentiële en logaritmische
functies)
Toepassing : Berekenen van logaritmen uit het hoofd
| a) |
2log 8 = 3 |
want 23 = 8 |
| b) |
4log 1 = 0 |
want 40 = 1 |
| c) |
10log 10 000 =
4 |
want 104 = 10 000 |
| d) |
10log (1/100)
= -2 |
want 10-2 = 1/100 |
| e) |
3log 27
= 3 |
want 33 = 27 |
| f) |
9log 3
= 1/2 |
want 91/2 = 3 |
| g) | 3log (1/81) = -4 | want 3- 4 = 1/81 |
de 'uitvinding' van logaritmen
In 1544 publiceerde de Duitse predikant Michaël Stifel zijn werk 'Aritmetica
integra' (volledige rekenkunde).
Hij noteert o.a. twee rijen
getallen, met daaronder de volgende tekst:
"Posset hic fere novus liber integer scribi de
mirabilibus numerorum, sed oportet,
ut me hic subducam et clausis oculis abea."
"Ik zou een geheel nieuw boek kunnen schrijven over de wonderbaarlijke
eigenschappen
van de genoteerde getallen,
maar bescheidenheid gebiedt mij met gesloten ogen daaraan voorbij te gaan."
|
Op de onderste rij staan machten van 2. De
bovenste getallenrij geeft de exponenten van die machten te zien. Stifel begreep dat hij met deze rij een aantal bewerkingen zou kunnen vereenvoudigen. Zo weten we : 2 . 8 = 16. Met de overeenkomende getallen uit de bovenste rij vormen we: 1 + 3 = 4. Hij maakte dus van een vermenigvuldiging een optelling In een tijd zonder rekenapparaatjes zou dit een aanzienlijke vereenvoudiging betekenen. Alleen moeten we nu van wel eerst van alle getallen weten welke macht van 2 het is. Begrijp je waarom Stifel er met gesloten ogen eraan voorbijging? |
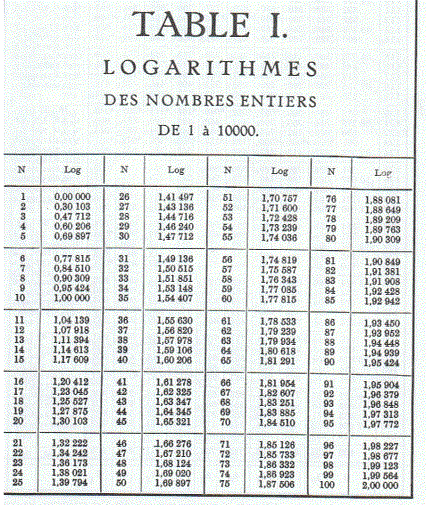Henry
Briggs schrok niet terug voor deze klus
Hij stelde in 1624 een tabel op met machten van 10.
Dergelijke 'logaritmetafels' werden tot in de jaren '70
op onze schoolbanken gebruikt…
|
naar startpagina |
|
oefeningen logaritmen oef.exp.vgln |