het begrip vector
Net zoals in het vlak, kunnen we ook in de ruimte met vectoren werken.
Twee punten A en B bepalen een gebonden vector .
Vectoren hebben een lengte, een richting en zin.
De vrije vector, bepaald door de vector  is de verzameling van alle gebonden vectoren
met dezelfde lengte, richting en zin.
Een gebonden vector die een vrije vector bepaald, noemen we representant van deze vrije vector.

 

som van vectoren
Het optellen van vectoren doen we grafisch als volgt:
geval 1 het eindpunt van de eerste vector is het beginpunt van de tweede vector:
De somvector heeft als:
beginpunt = het beginpunt van de eerste vector
eindpunt = het eindpunt van de tweede vector



geval 2 de twee vectoren hebben eenzelfde beginpunt:
We tekenen een parallellogram met de twee vectoren als zijde.
De som vinden we als de diagonaal van dit parallellogram.



geval 3 de ligging van de twee vectoren is willekeurig:
Een van de twee vectoren verschuiven we,
zodat de twee vectoren hetzelfde beginpunt hebben.
Met een parallellogram vinden we de somvector.

veelvoud van vectoren
Het product van een vector met een reëel getal r is een vector r . met
- dezelfde richting als 
- dezelfde zin als     als r >0  en tegengestelde zin als r < 0
- als lengte = | r | . de lengte van
We noemen dit een scalaire vermenigvuldiging.

opm: voor r = 0 vinden we 0. =
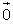
r . 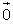=