zwaartepunten en integralen wiskunde-interactief.be

Moment
De mechanica bestudeert beweging en arbeid onder invloed van krachten die erop werken.
Hierbij is niet alleen de grootte van de kracht belangrijk, maar ook het aangrijpingspunt.
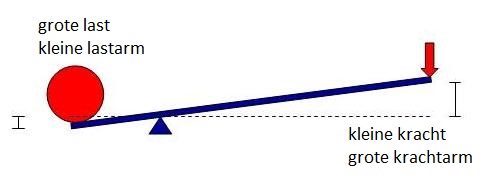
Bij hefbomen weet je dat je met een kleine kracht een grote last kunt optillen.
Hierbij is het product last . lastarm gelijk aan het product kracht . krachtarm.
In de mechanica noemt met deze producten moment .

Wanneer we de resultante van meerdere krachten willen berekenen, moet
- de grootte van de resultante gelijk zijn aan de som van de grootte van de afzonderlijke krachten.
- het moment van de resultante gelijk zijn aan de som van de momenten van de afzonderlijke krachten.

 

Zwaartepunt
Heel wat vraagstukken kunnen we herleiden tot een kracht die inwerkt op een punt: het zwaartepunt.
Het zwaartepunt van geometrische figuren als cirkels en vierkanten kennen we.
Bij andere vormen moeten we eerst berekenen waar dat zwaartepunt ligt.
Hiervoor berekenen we een krachtenevenwicht en een momentenevenwicht.
De grootte en het moment van de resultante moet gelijk zijn aan de som van de krachten op elk deel
van de figuur afzonderlijk en hun moment.
De zwaartekracht op een figuur is evenredig met zijn oppervlakte.




Zwaartepunten en integralen
Bij figuren die begrensd zijn door de grafiek van een functie kan je gebruik maken van integralen.
We berekenen het zwaartepunt van een kwart cirkel.

naar startpagina naar sitemap  primitieve functie overzicht integralen

moment   zwaartepunt   integralen

oefeningen integralen opgeloste oefeningen oefeningen analyse