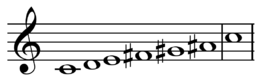van sinusfuncties tot een toonsysteem wiskunde-interactief.be

.

Geluid
Geluid is de waarneming van een verandering van druk in de lucht of een ander medium, b.v. water.
Deze verandering plant zich voort door dit medium als een golf.
Grotere drukveranderingen nemen we waar als een luidere toon.
Snellere drukveranderingen nemen we waar als een hogere toon.

Een wiskundig en natuurkundig extra : waarom wordt geluid voorgesteld door sinusfuncties?       Om een snaar (of ons trommelvlies) te laten trillen, moeten we een kracht uitoefenen. - Deze kracht is (meestal en ongeveer...) evenredig met de uitwijking van snaar of trommelvlies, zodat:   F = - k . y   (met F = kracht, - y = uitwijking  en k = evenredigheidsconstante) - We kennen ook de eerste wet van Newton:   F = m . a (met F = kracht, m = massa en a = versnelling) - Stellen we beide gelijk aan elkaar, dan krijgen we   m . a = - k . y   m . a + k . y = 0 - Wiskundig kan je de versnelling a schrijven als d2y/ dt2 en dus:   d2y/ dt2 + k . y = 0   Een dergelijke vergelijking noemt men een differentiaalvergelijking.   Je lost differentiaalvergelijkingen op door functies te zoeken die voldoen aan de vergelijking.   Vergelijkingen die voldoen aan deze vergelijking zijn van de vorm y = a . sin ( b. t + c) - In de praktijk zal geluid bestaan uit een stapeling van meerdere sinusfuncties en ruis.   Toch blijft de eenvoudige sinusfunctie de basis om geluid en muziek te bestuderen. Een zeer uitvoerige wetenschappelijke behandeling van het onderwerp geluid en muziek vind je in het boek: Music: A Mathematical Offering (Dave Benson, University of Aberdeen Scotland, UK). De auteur behandelt zowel het produceren van geluid door verschillende types van instrumenten als de evolutie van toonsystemen en stemmingen doorheen de muziekgeschiedenis. Je vindt het boek ook digitaal op het internet. Het pdf-document op http://hps4000.com/pages/special/sound_history.pdf  geeft een goed overzicht van de geschiedenis van geluidsmeting.

In periodieke functies wordt een patroon (de rode golf binnen de groene rechthoek) periodiek herhaald . - De sinusfunctie f(x) = a sin (bx) golft rond de x-as. We noemen deze as de evenwichtslijn.  - De maximale uitwijking t.o.v. de evenwichtlijn noemen we de amplitude. - De versleepbare groene rechthoek bakent het patroon af dat zich herhaalt.    De lengte van dit patroon noemen we de periode van de functie.

In geluidsgolven bepaalt de amplitude de geluidssterkte en de periode de toonhoogte.
Een trilling met een kortere periode trilt sneller en nemen we waar als een 'hogere' toon.
Het aantal trillingen per seconde noemt men de frequentie, met als eenheid Herz (Hz).

Welk voorschrift komt overeen met welke frequentie?

Doppler effect
Misschien kende je de naam niet, het effect ken je zeker.
Wanneer een wagen voorbijrijdt, daalt het geluid dat je hoort plots na het voorbijrijden.
Hoe groter de snelheid, hoe groter het geluidsverschil.
Dit effect is genoemd naar de Oostenrijker Christian Doppler die het midden de 19e eeuw beschreef.
Ook hier moeten we kijken naar wat er gebeurt met de geluidsgolven van een bewegende bron.


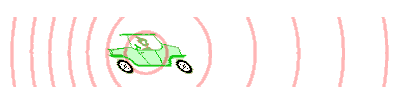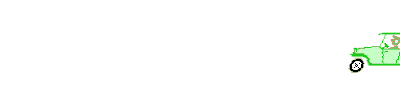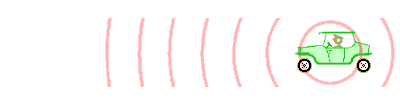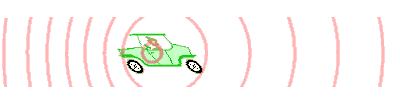
Elke golf van de naderende auto doet er een welbepaalde tijd over om de waarnemer te bereiken.
De volgende golf moet een iets kleinere afstand afleggen, omdat de auto nu dichterbij is.
De waarnemer ontvangt de golven in een net iets hogere frequentie dan wanneer de auto stilstaat.
Dat komt neer op een toon die iets hoger lijkt te zijn.
Bij het voorbijrijden, wordt de naderende auto een zich verwijderende auto.
De golven doen er nu iets langer over. De toon lijkt nu lager.
De waargenomen frequentie bij een bewegende bron wordt:

fwaarneming = fbron . (	v	)            bij naderen
	v - vbron
fwaarneming = fbron . (	v	)            bij verwijderen
	v + vbron

In deze formules staat v voor de snelheid van het geluid.
Deze is afhankelijk van temperatuur en luchtvochtigheid, maar in een grootteorde van 335 m/s of 1200 km/u.
Een la van 440 Hz klinkt bij een naderingssnelheid van 100 km/u als 480 Hz, dat is iets tussen sib en si.  
Een la van een verwijderende bron aan 100 km/u klinkt als 406 Hz, bijna zo laag als een sol.

Een toonsysteem
Theoretisch kan je elke willekeurige frequentie combineren tot muziek.
Toch zingt ieder van ons zonder problemen do-re-mi-fa-sol-la-si-do mee met de Sound of Music.
Om samen muziek te maken, kunnen we niet zonder
- een systeem van tonen die bij elkaar passen.
- een referentietoon voor muzikanten en instrumentenbouwers.

Tot de 19e eeuw is er geen sprake van een internationale standaard. Zelfs lokaal worden verschillende toonhoogten gebruikt. In de 18e eeuw worden de eerste stemvorken gemaakt, maar steeds nog zonder erkende standaard. In de 19e eeuw leggen meerdere landen eigen standaarden vast, maar internationaal blijft het wachten tot  1955,     wanneer het ISO (International Organisation for Standardization) de la (A) = 440 Hz aanneemt als norm. Toch is er een een trend om in symfonische orkesten de la iets hoger te nemen. Reeds in 6e eeuw gebruikte de filosoof Boetius de letters van het Latijns alfabet als naam voor de opeenvolgende tonen, startend met de A voor de toon die wij la noemen. Onze notennamen komen van de monnik Guido van Arezzo die rond het jaar 1000 een bekende hymne gebruikte.  De tekst luidt: ut(do) queant laxis resonare fibris mira gestorum famuli tuorum solve polluti labii reatum Sancte Iohannes De hymne begint iedere regel een secunde hoger. Guido gebruikte de beginlettergrepen ut-re-mi-fa-sol-la en begon dus niet met de la (A) In de 19e eeuw werd ut vervangen door ‘do’ en noemde men de 7e trap si.

Toets je op een piano een la in, dan neem je dus een luchtdrukgolf waar die 440 keer per seconde trilt.
Op een piano staat niet een maar meerdere la's:


De toonafstand tussen twee opeenvolgende la's noemt men een octaaf.
Speel je een la een octaaf hoger, dan klinkt een trilling met een frequentie die tweemaal zo hoog is.
Speel je een la een octaaf lager, dan is de frequentie van de trilling maar half zo groot.

De naam octaaf verwijst naar het cijfer 8.
Ons toonsysteem is inderdaad opgebouwd uit toontrappen, waarbij het octaaf de 8e trap is.
De tonen tussen de la van 440 Hz en zijn octaaf van 880 Hz hebben een frequentie daar tussenin.
De toontrappen binnen een octaaf worden in stijgende volgorde genummerd.
De grondtoon noemt men prime. Verder volgen secunde, terts, kwart, kwint, sext en septiem.

Deze acht opeenvolgende trappen vormen een toonladder.

Toonladders
Zing of speel eens een toonladder. De kans is groot dat je iets krijgt als:

Deze zogenaamde grote tertstoonladder is een opeenvolging van 7 stamtonen do-re-mi-fa-sol-la-si.

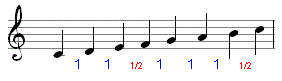
Deze opeenvolging komt op een piano overeen met de naast elkaar liggende witte toetsen.
Merkwaardig is dat de afstanden tussen de verschillende tonen niet even groot is.
De afstand tussen de 1e toon (do) en de 2e (re) is een hele toon.
De afstand tussen de 3e toon (mi) en de 4e (fa) is maar een halve toon.
Dit lijkt heel onlogisch. Waarom twee keer een halve toonafstand nemen?
Als je die twee halve toonafstanden zou samenvoegen zouden alle toontrappen toch even groot zijn...
Het laatste waarvan je Pythagoras zou verdenken is niet logisch te denken.
Pyhtagoras onderzoekt welke samenklinkende tonen als welluidend worden ervaren: zie Samenklanken.
Deze samenklanken gebruikt hij om de toontrappen binnen een octaaf te bepalen: zie Pythagoras.

Toch kunnen we ook in stapjes van halve tonen van do naar do:

Op de piano speel je deze toonladder door ook de zwarte toetsen op te nemen in de stijgende reeks.
Deze toonladder met halve toonstapjes noemt men de chromatische toonladder.
De bijkomende tonen krijgen geen eigen namen.
Men gebruikt het teken # om de verhoging met een halve toon aan te duiden.
De toonladder met enkel de stamtonen noemt men de diatonische toonladder. 
En een kritische geest die 'grote tertstoonladder' hoort, denkt meteen:
"Bestaat er dan ook een kleine tertstoonladder?"
Jawel hoor. Neem voor de afstand tussen 2e en 3e trap een halve toon en je krijgt dit:

Naast het verhogingsteken # betekent een b dat een toon met een halve toon verlaagd wordt.
Voor de volledigheid: dit is de 'stijgende melodische kleine tertstoonladder'.
In de 'harmonische kleine tertstoonladder' is ook de si verlaagd naar een sib.
In de 'natuurlijke kleine tertstoonladder' zijn zowel de si als de la verlaagd naar sib en lab.

In dezelfde opeenvolging van hele en halve tonen kunnen we ook starten vanuit andere tonen dan een do.
Hierbij kan je de kwintencirkel volgen:

Twee toonsoorten die een kwint uit elkaar liggen hebben 6 van de 7 tonen gemeen. Volg je de kwintencirkel in wijzerzin, dan verschijnt er in de voortekening aan de sleutel telkens 1 kruis extra. Volg je de kwintencirkel tegenwijzerzin dan verschijnt er in de voortekening aan de sleutel telkens 1 mol extra. Je vertrekt hierbij van de toonladder in do groot (C): do - re - mi - fa - sol - la - si - do. We doen vanaf C één stap in wijzerzin en komen uit op sol groot (G) Je krijgt dus 1 verhoogde toon: fa#. sol - la - si - do - re - mi - fa# - sol. Doen we vanaf C één stap in tegenwijzerzin, komen we uit op fa groot (F) Je krijgt dus 1 verlaagde toon: sib. fa - sol - la - sib - do - re - mi - fa. In de kleine tertstoonladders krijg je eenzelfde verhaal door te starten met de toonladder van la klein (a).

Reeds in de Griekse Oudheid bepaalde men de frequenties van deze stappen vanuit verhouding met
de frequentie van de grondtoon. Toonafstanden met deze verhoudingen noemt men ‘rein’.

beginnend met do als grondtoon:	do	re	mi	fa	sol	la	si	do
rangorde	prime	seconde	terts	kwart	kwint	sext	septime	oktaaf
frequentieverhouding met de prime is	1/1	9/8	5/4	4/3	3/2	5/3	15/8	2/1

andere verdelingen
Een toonladder verdeelt de afstand tussen grondtoon in een aantal trappen.
Wij zijn zo gewoon aan 'onze' toonladder, dat we er nauwelijks bij stilstaan dat het ook anders kan.
Zo kan je het octaaf ook onderverdelen in gelijke intervallen.
Tel je enkel in hele tonen, dan krijg je de hele toonstoonladder:

De toonladder ziet uit als volgt:

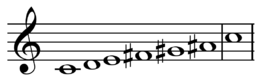
Deze toonladder heeft dus een toon minder dan de vorige toonladders.
Bovendien staat ook de kwint van de grondnoot (de sol) er niet in, maar wel een sol#.
Eigenlijk mag je doen wat je wil.
Je kan een octaaf ook onderverdelen in 2 of 3 of 11 of 17...
Vraag is "Hoe klinkt de muziek die je er mee kunt maken?"
Doorheen de geschiedenis hebben muziekwetenschappers, wiskundigen en componisten heel wat uitgeprobeerd
en muzieklandschappen verkend die er heel anders uitzagen dan do-re-mi-fa-sol-la-si-do.

pentatonische toonladder
Zoals de naam al doet vermoeden, is de pentatonische toonladder opgebouwd uit 5 tonen.
Stapel je vanaf de grondtoon C(do) 4 kwinten op elkaar, dan krijg je C - G - D - A - E.
Herleid je die tonen naar eenzelfde oktaaf, dan krijg je de opeenvolging C - D - E - G - A:

Je kan de verschillende tonen verkennen in volgend bestand.
Hij klinkt wat oosters in onze oren en op het eerste zicht beperkt in zijn mogelijkheden.
Maar meer dan deze 5 tonen heb je niet nodig om b.v. het thema van de 'Morgenstimmung' van Grieg te spelen.


Je kan de reeks ook beginnen vanaf F, de onderkwint van C;
Je krijgt dan als reeks F - C - G - D - A.
Herleid je die tonen naar eenzelfde octaaf, dan krijg je de opeenvolging F - G - A - C - D.
En speel je deze tonen een halve toon hoger, dan vallen ze samen met de vijf zwarte toetsen op een pianoklavier.

-