een muzikale zoektocht
wiskunde-interactief.be
Het geheel rond sinusfuncties, geluid en
muziek is uitgewerkt op acht pagina's:
-
van
sinusfuncties tot een toonsysteem schetst
de natuurkundige en wiskundige basis van geluid.
-
samenklanken
en verhoudingen beluistert en onderzoekt
het resultaat van samenklinkende geluiden.
-
boventonen
en zwevingen onderzoekt
het voorkomen van natuurlijke boventonen en het
waarnemen
van zwevingenbij tonen die nauwelijks van elkaar verschillen.
-
de kwinten
van Pythagoras ontleedt hoe Pythagoras
vanuit kwintverhoudingen een toonladder opbouwt.
-
het komma
van Pythagoras' ontleedt hoe Pythagoras
vanuit kwintverhoudingen een toonladder opbouwt.
-
een
muzikale zoektocht' volgt de
muziekgeschiedenis in zijn zoektocht naar
welluidendheid.
- barokstemmingen'
ontleedt enkele pogingen om nieuwe oplossingen
te vinden voor nieuwe muzikale wensen.
-
de
kettingbreuk van Huygens' ontleedt Huygens'
berekeningen om een 'juister' klinkende
toonladder uit te bouwen.
Extra: partituurfragmenten en youtube-filmpjes
illustreren de theorie.
-
de zoektocht in klank en beeld:
opmerking over het afspelen
van geluid:
GeoGebra is in de eerste plaats een fantastisch
wiskundeprogramma maar geen gesofisticeerd
keyboard.
Verschijnt er bijvoorbeeld in een grijs scherm
een foutmelding over het afspelen, herlaad dan
gewoon de pagina en
klik gewoon opnieuw op 'speel'. Doe hetzelfde
wanneer je het afspelen van een geluid niet kan
stoppen.
Hoor je geen geluid, probeer dan eens een andere
browser...
Zelfs met deze gebreken is het een unieke manier
voor wiskundigen om iets over muziek te leren en
omgekeerd. |
Kerktoonladders
"Zing of speel
eens een toonladder".
De kans is groot dat je op deze vraag iets te horen krijgt als do - re - mi -fa
- sol -la - si - do.
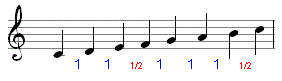
Deze zogenaamde
'grote tertstoonladder'
is een opeenvolging van 7 stamtonen do-re-mi-fa-sol-la-si.
Wanneer we een toonladder zingen, plaatsen we spontaan dezelfde afstanden van
hele en halve tonen
op dezelfde plaatsen in de toonladder, met welke toon we ook beginnen.
Zo zingen we 'la - si - do# - re - mi - fa# - sol# - la' zonder te moeten
nadenken over toonafstanden.
In de middeleeuwen kende men deze opeenvolging, maar men ging er ander mee om.
In de middeleeuwse kerktoonladders hangt de afstand tussen de tonen niet af van
de plaats binnen de toonladder.
Wanneer een toonladder begint met een andere toon dan do worden tonen niet
verhoogd of verlaagd.
De volgorde waarin hele en halve tonen elkaar afwisselen hangt dus af van de
begintoon.
De reine stemming kent grote en kleine hele tonen, afhankelijk van de plaats in
de toonladder.
Een 'juiste' reine stemming in C klinkt vals in een andere toonaard, omdat de
verhoudingen niet meer kloppen.
Omdat in de kerktoonladders de afstanden niet afhangen van de plaats in de
toonladder kennen ze dat probleem niet.
Is de toonladder juist gestemd in C, dan klinken meteen ook alle andere
toonaarden juist.
Renaissance - de terts verschijnt
In de 16e eeuw schrijven componisten als Lassus heel vernieuwende
muziek.
De steunpunten van zijn composities zijn samenklanken die niet alleen op kwinten
en octaven gebaseerd zijn,
maar op drieklanken, gevormd door grondtoon – terts – kwint.
De terts wordt niet langer vermeden als ‘vals klinkend’, maar wordt juist
een middel om een samenklank te kleuren.
Tot op vandaag blijft de samenklank grondtoon – terts – kwint de basis waarop
gecomponeerd wordt,
zowel in de klassieke muziek als in basisgitaarakkoorden.
Het probleem dat tertsen, kwinten en octaven nooit samen als rein kunnen gestemd
worden, was al lang bekend.
Maar het is nu pas dat het echt een probleem wordt.
De reine stemming liet de afhankelijkheid van kwinten los
en definieert een tertsverhouding gewoon als 5/4. Hierdoor is elke hele
toonafstand niet meer even groot en
kan je niet zomaar veranderen van toonaard. Muziekwetenschappers en wiskundigen
staan voor een grote uitdaging.
Is er een mogelijkheid om rein te spelen en toch muziek te kunnen maken in
verschillende toonaarden?
Ze volgen hierbij twee sporen:
1. We zoeken een systeem waar
zoveel mogelijk tonen rein klinken en laten tonen
in verafgelegen toonaarden vals.
Deze stemmingen noemen we ongelijkzwevend, want de onzuiverheden zijn niet
voor alle tonen gelijk.
2. Om in alle mogelijke toonaarden te kunnen spelen verdelen we de
onzuiverheden
gelijk over alle tonen.
Deze stemmingen noemen we daarom gelijkzwevend.
Een systeem waarin in elke toonaard elke toonafstand gelijk is, werd al in die
16e eeuw uitgewerkt als theoretisch concept,
maar men zal er enkele eeuwen over doen eer het
algemeen ingang vindt in onze ‘gelijkzwevende stemming’.
Renaissance - de terts verschijnt
De tertsen, die vanaf de renaissance op de voorgrond verschijnen, krijgen nu ook
meer wiskundige aandacht.
“Hoe krijg je binnen een werkbaar toonsysteem een terts rein?” wordt de
kernvraag.
In middentoonstemmingen
willen we de terts rein, maar zonder de kwintafhankelijkheid op te geven.
De middentoonstemming lijkt ei van Columbus voor het stemmingsprobleem.
In plaats van (zoals Pythagoras) vast te houden aan reine kwinten en de reine
tertsverhouding op te geven,
draait men de rollen om. Men geeft de reine kwintverhouding op om reine tertsen
te krijgen.
Dat kan enkel gerealiseerd worden door de kwint iets kleiner te maken.
Een rekensom: Hoe groot moet een kwint zijn zodat 4 kwinten : 2 octaven
uitkomt op 5/4?
Oplossing: De kwintverhouding moet dus iets verkleind worden, nl. van 3/2 (= 1,5) tot 4√5
= 1,4953
Dit is wiskundig mooi gevonden, want de tertsverhouding komt nu perfect uit op
5/4:
4 kwinten : 2 octaven wordt nu immers = 4√5
x 4√5 x 4√5 x 4√5 :4 = (4√5)4
: 4 = 5 : 4.
Resultaat:
- De terts is perfect rein.
- De kwint is iets te klein maar wijkt nauwelijks af van de 3/2 verhouding.
- Alle afstanden kunnen berekend worden vanuit de kwint.
- De afstanden C-D en D-E zijn even groot en niet meer grote en kleine zoals in
de reine stemming.
- Omdat de kwint niet helemaal perfect is, verschilt de klankkleur van de
verschillende toonaarden.
Dit wordt bewust gebruikt door componisten in de keuze van een toonaard.
In volgende tabel kan je het resultaat van deze middentoonstemming aflezen.
| toontrap |
berekening
door kwinten |
verhouding
frequenties |
frequentie
la = 440 Hz |
frequentie
rein |
frequentie
gelijkzwevend |
| prime (C) |
C |
1/1 |
1/1 |
440 Hz |
440 Hz |
440 Hz |
| secunde (D)
|
C - G - D
2x kwint : 1 octaaf terug |
4√5 x 4√5 : 2 |
1,118 |
492 Hz |
495 Hz |
494 Hz |
| terts (E) |
C - G - D - A - E
4x kwint : 2 octaven terug |
(4√5)4
: 4 |
5/4 |
550 Hz |
550 Hz |
554 Hz |
| kwart (F) |
F - C
dalende kwint van octaaf |
2 : 4√5 |
1,3375 |
588 Hz |
587 Hz |
587 Hz |
| kwint (G) |
C - G |
4√5 |
1,49535 |
658 Hz |
660 Hz |
659 Hz |
| sext (A) |
C - G - D - A
3x kwint : 1 octaaf terug |
(4√5)3 : 2
|
1,672 |
735 Hz |
733 Hz |
740 Hz |
| septime (B) |
C - G - D - A - E - B
5x kwint : 2 octaven terug
|
(4√5)5 : 4
|
1,87 |
822 Hz |
825 Hz |
830 Hz |
| otaafc (C) |
C - C |
2/1 |
2/1 |
880 Hz |
880 Hz |
880 Hz |
en zo klinkt het:
In de kwintverhouding 4√5 wordt de kwint met 1/4 van een komma
(= 1/9 van een hele toon) verkleind.
De correcte benaming is daarom de 1/4 komma-middentoonstemming.
Want er bestaan ook 1/5 en 1/6 komma middentoonstemmingen waarbij de kwint minder
sterk verlaagd wordt.
Dit zijn compromissen tussen kwint en terts. De tertsen klinken minder zuiver,
maar de kwint dan weer iets zuiverder.
Barok - de middentoonstemming 'bijgestemd'
Waarom deze alternatieven als met een kwintverhouding 4√5 de terts
rein klinkt en dus alles in orde lijkt?
Met een kwintverhouding 3/2 komen 12 kwinten uit op (3/2)12 = 129,7
tegen (2/1)7 = 128 voor 7 octaven.
De kwint is dus te groot en de kleinere middentoonkwint lijkt een goed middel om
dit te verhelpen.
Maar met een kwintverhouding
4√5 komen
12 kwinten uit op ( 4√5)12
= 125 ...
wat dan weer dramatisch te klein is.
Silbermann
De 18e eeuwse orgelbouwer Silbermann besluit de kwint iets minder te verlagen
dan de 1/4e komma.
De terts is nu niet helemaal rein, maar de kwintencirkel sluit op het eind beter
aan.
Werckmeister
Een tweede alternatief is 4√5 aan te houden, maar ze niet op
alle kwinten toe te passen.
Eveneens begin18e eeuw past Werckmeister deze methode toe.
Hij gebruikt in zijn kwintencirkel 4 middentoonkwinten en 8 reine kwinten.
Voor het totaal van 12 kwinten is het resultaat: (4√5)4 . (3/2)8
= 128,14 tegenover 128 voor 7 oktaven.
Zijn verdeling van de kwintverhoudingen binnen de kwintencirkel is:
| C - G |
G - D |
D - A |
A - E |
E - B |
B - Fis |
verder |
4√5
middentoon |
4√5
middentoon |
4√5
middentoon |
3/2
rein
|
3/2
rein
|
4√5
middentoon |
6 keer 3/2
rein |
De middentoonkwinten sluiten niet op elkaar aan.
Voor de terts C - E krijg je nu door een opeenstapeling van 3 middentoonkwinten
en 1 reine kwint.
Ze heeft een verhouding (4√5)3 . (3/2) : 4 = 1,254
wat nauwelijks meer is dan de reine verhouding 1,25.
Door de schikking van de 4 middentoonkwinten neemt de nauwkeurigheid van de
tertsen af voor tertsen die
verder in de kwintencirkel liggen.
- Voor de tertsen op G en D krijg je (4√5)2 .
(3/2)2 : 4 = 1,258 i.p.v. het reine 1,25.
- Voor de tertsen op A, E en B krijg je 4√5 . (3/2)3
: 4 = 1,262.
- Voor alle andere tertsen krijg je (3/2)4 : 4 = 1,266.
Met deze stemming kan je alle toonaarden spelen omdat de verschillen met de
reine afstanden klein blijven.
De verschillende combinaties van grotere en kleinere tertsen en/of kwinten geven
elke toonaard zijn eigen kleur.
Enkele van deze ongelijkzwevende stemmingen worden meer gedetailleerd vergeleken op
barokstemmingen.
In zijn werk 'Ideen zu einer Aesthetik der Tonkunst' uit 1806 associeerde de
Duitse auteur Christian Schubart de
verschillende toonaarden met verschillende gevoelens:
|
Voortekening: |
/
3b
1b
4#
2#
1b
3b
6#
4#
1#
1b
4b
6#
3#
1#
2b
4b
7b
3#
/
2b
5b
5#
2# |
C:
puur, onschuldig, naïef
c
klein:
smachtend zuchten van de naar liefde verlangende
ziel.
Dmol:
sluw, maar ook smartend en vervoerend.
kan niet lachen maar glimlachen, niet janken
maar heeft een wenende grimas.
een toonaard voor ongewone karakters en
gevoelens
c#
klein:
boetende klaagzang,
intieme conversatie met God, zuchten naar
ontgoochelende vriendschap.
D:
triomf, victorie, marsen, vakantieliederen en
hemelbezingende koorzang
d
klein:
melancholieke vrouwelijkheid
Emol:
liefde en toewijding
d#
klein:
angstgevoelens en wanhoop.
Als geesten konden spreken, zouden ze deze
toonaard gebruiken.
E:
uitbarsting van vreugde en genot maar nog niet
volledig geluk
e
klein:
naïeve, vrouwelijke liefdesverklaring, zuchten
met enkele tranen, hoop op het geluk van
toonaard C
F:
minzaamheid en kalmte
f
klein:diepe
depressie, sombere klaagzang en verlangen naar
het graf
F#:
triomf van de overwinning na een zware
strijd
f#
klein:
dreigend als een hond die zich vastbijt
G:rustiek,
idyllisch, lyrisch, de kalmte van voldane
passie, dankbaarheid voor trouwe vriendschap en
liefde,
alle vredevolle emotie van het hart
g
klein:
ontevreden, zorgen makend, slecht gehumeurdheid,
wrok
Amol:
toonaard van het graf, het Laatste Oordeel en de
eeuwigheid
amol klein:
mopperend, klagend, alles wat te maken heeft met
het vechten tegen moeilijkheden
A:
verklaring van onschuldige liefde, tevredenheid,
hoop op het weerzien bij het afscheid,
godsvertrouwen
a
klein:
vrome vrouwelijkheid en tederheid
Bmol:
opgewekte liefde, hoop
op een betere wereld
bmol klein:
nors, spottend met
God, ontevredenheid met zichzelf en alles,
zelfmoordgedachten
B:
felgekleurd, wilde passies aankondigend, woede,
jaloersheid, wanhoop en al wat op het hart drukt
B
klein:
geduldig, het lot afwachtend |
In toonaarden met minder wijzigingstekens benaderen de tonen van de toonaard
beter de reine verhoudingen.
Een componist zal dus toonaarden met veel wijzigingstekens vermijden ... tenzij
hij juist een expressief effect
wil bereiken met toonafstanden die minder rein klinken.
Toonaarden met veel wijzigingstekens worden dan ook niet zomaar geassocieerd met
passie, woede of dood.
Barokcomponisten als J.S. Bach buiten dit verschil expressief uit door telkens
de 'geschikte' toonaard te kiezen.
In de Mattheuspassie, waarin Bach het lijdensverhaal van Christus verklankt in
een 3 uur lange compositie,
volgen objectief vertellen, kwaadheid, verdriet, bezinning elkaar af.
Bach schrijft zijn
compositie niet in één vaste toonaard, maar
volgt de gevoelens van de tekst.
Voor de verhalende passages gebruikt hij
toonaarden met slecht 1 of 2 wijzigingstekens.
De meest expressieve passages staan in minder
gebruikelijke toonaarden met meer
wijzigingstekens.
Voorbeelden zijn het stuk waar de dood van Jezus
beschreven wordt en de koorpassages waarin de
onschuld van
Jezus in contrast geplaatst wordt met de
zondigheid van de mens. |
31-tonensysteem van Christiaan Huygens
Een tweede benadering is: "Kunnen we een oktaaf zo onderverdelen dat alle
toontrappen gelijk zijn en tegelijk
rein (of toch minstens zo rein mogelijk) klinken?"
Net zoals in de tijd van Pyhtagoras zijn het ook nu wiskundigen en
natuurkundigen die aan de kar trekken,
zoals de vader van Galileo Galilei, Simon Stevin, Christiaan Huygens, Descartes
en Leonard Euler.
Hun benadering komt er op neer een oktaaf in zoveel stapjes onder te verdelen
dat de kwint samenvalt
met een van die stapjes en liefst ook de kwart en de terts.
Huygens gebruikt een kettingbreuk om de kwintverhouding 4√5 van de middentoonstemming te noteren.
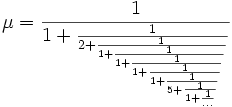
De gedachte achter de kettingbreuknotatie is dat een reëel getal de som is van een
geheel getal en een getal
tussen 0 en 1.
Dit deel kan geschreven worden als een breuk.
Deze breuk schrijven we als het omgekeerde van zijn omgekeerde: a/b = 1/(b/a).
Het uitwerken van b/a geeft weer een decimaal getal, enzovoort.
Zo ontstaat een kettingbreuk.
Elke stap in de benadering noemt men een convergent en vormt een breukbenadering
van het decimaal getal.
Huygens vond de breuken: 1/2 3/5 4/7 7/12 11/19
18/31 101/174 119/205.
Meer uitleg over kettingbreuken en de benadering van Huygens vind je op
de kettingbreuk van Huygens
Je kan een oktaaf dus onderverdelen in 205 stapjes, maar instrumenten maken met
deze verdeling is wat anders.
Huygens stelt voor om een oktaaf in
31 toontrappen te verdelen,
zodat je op elk instrument muziek kan spelen in om het even welke toonaard.
Joan Albert Ban, priester en bevriend met Descartes en Huyghens, ontwikkelde het
"Volmaekte Klaeuwier".
Omdat de afstand tussen de tonen en de omvang niet te groot zou worden, ontwerpt
hij tussenliggende toetsen
die boven elkaar liggen in verschillende rijen.

De benaderingen van kwint, kwart en terts van Huygens zijn heel knap.
| toontrap |
verhouding
Huygens |
verhouding
rein |
frequentie
Huygens |
frequentie
rein |
frequentie
gelijkzwevend |
| kwint |
2(18/31) = 1,4955
|
3/2 = 1,5 |
658 Hz |
660 Hz |
659 Hz |
| kwart
|
2(13/31) = 1,3373 |
4/3 = 1,333 |
588 Hz |
587 Hz |
587 Hz |
| terts |
2(10/31) = 1,2505 |
5/4 = 1,25 |
550 Hz |
550 Hz |
554 Hz |
Ban kon zo onzuiverheden opvangen zonder compromissen te doen, maar een succes
werd zijn uitvinding niet.
Het instrument bleek toch niet zo praktisch.
De gelijkzwevende stemming in een toonladder met 12 stappen
wiskunde en
muziekpraktijk
Muziek binnen een beperkte toonomvang en in een vaste toonaard kon het best
stellen met de reine stemming.
In de 16e eeuw doet men de eerste pogingen om de verschillen tussen de
toonafstanden weg te werken,
zodat
men tenminste in verschillende toonaarden zou kunnen spelen.
In verschillende pogingen worden compromissen en streefdoelen in de weegschaal
gelegd.
Ook de Kerk moeit zich, want die vindt kerkorgels die onzuiver gestemd zijn niet
kunnen.
Het theoretisch denken en de muziekpraktijk evolueren geleidelijk naar een
systeem waarin de onderlinge
verhoudingen binnen alle toonaarden gelijk zijn en men vrij is om toonaarden te
kiezen.
In de muziek wordt de samenklank belangrijker dan de melodie en het wijzigen van
toonaard binnen een compositie
wordt gebruikt als expressief middel.
De oplossing hiervoor vindt men in het verdelen van de onzuiverheden over alle
halve tonen van een octaaf. |
Deze verdeling bleek een beter compromis tussen juistheid en het praktische.
De verdeling in 12 trappen is de gelijkzwevende stemming van onze chromatische
toonladder:
do(1) - do#(2) - re(3) - mi(4) - fa(5) - fa#(6) - sol(7) -
sol#(8) - la(9) - la#(10) - si(11) - do(12).
In 12 stapjes ga je van do naar do.
In deze gelijkzwevende stemming is bijvoorbeeld sol# gelijk aan lab en dat laat
overgangen tussen toonaarden toe.
In grote orkestwerken als een symfonie werd het gebruikelijk om binnen een werk
meerdere keren te veranderen
van toonaard en een hele evolutie van toonaarden uit te bouwen.
Maar ook in populaire muziek is het niet ongebruikelijk dat in een kort
instrumentaal bruggetje de toonaard verandert
en een refrein nog een keer klinkt, maar nu een halve toon hoger.
Van fluiten en composities die beperkt waren tot een vaste toonaard evolueert
dus tegelijk de muziektheorie,
de composities en de instrumenten tot een flexibel systeem van uitwisselbare
toonaarden.
We gaven hierbij wel de absoluutheid van reine intervallen op...
Hoe verdelen we dan een oktaaf in 12?
Oktaven vinden we door de frequentie van een toon telkens te vermenigvuldigen
met 2.
We zitten dus niet met een lineaire functie maar met een exponentiële functie.
De frequentie van opeenvolgende la's vind je als
fn = 440 . 2n
De tussenliggende tonen berekenen we als tussentrapjes van deze factor 2:
Gelukkig zijn er nog de zwevingen
Wat wordt dan het verschil tussen een dergelijke gelijkzwevende kwint en de niet
gecorrigeerde?
De kwint van een la op 440 Hz is een mi, maar wat wordt haar frequentie?
Met de reine verhouding 3/2 komen we uit op fmi = 3/2 . 440 =
660
Hz.
In de gelijkzwevende stemming is de kwint de 7e trap met als frequentie fmi
= 440 . 2(7/12) =
659.255 Hz
Het frequentieverschil tussen de reine en de gelijkzwevende toon geeft precies
het aantal zwevingen dat je moet
horen wanneer je een piano gelijkzweving wil stemmen. Hier hoor je dus
0.745 zwevingen per seconde.
En zo blijken afwijkingen toch nog nuttig.
Volgend bestand illustreert hoe beide mi's klinken.
Apart lijken ze even hoog, maar samenklinkend hoor je de zwevingen.
Turkse klassieke muziek
Een verdeling in 12 is een mogelijke keuze, maar niet de enige.
Een mooi voorbeeld is de Turkse klassieke muziek.
Een oktaaf wordt hier in 53 gelijke stukjes verdeeld, die men 'koma' noemt.
Benaderingen voor de stamtonen worden berekend als 2(.../53).
In volgende kolom kan je deze benaderingen vergelijken met reine en
gelijkzwevende verhoudingen.
De verdeling in 53 trappen laat betere benaderingen toe dan een verdeling in 12
halve toontrappen.
| interval |
berekening |
resultaat |
rein |
gelijkzwevend |
| secunde |
2(9/53) |
1,1249 |
9/8 =
1,125 |
1,1225 |
| terts |
2(17/53) |
1,249 |
5/4 =
1,25 |
1,2599 |
| kwart |
2(22/53) |
1,3338 |
4/3 =
1,333 |
1,3348 |
| kwint |
2(31/53) |
1,49994 |
3/2 =
1,5 |
1,4983 |
| sext |
2(40/53) |
1,687 |
5/3 =
1,667 |
1,6818 |
| septime |
2(48/53) |
1,8734 |
15/8 =
1,875 |
1,8877 |
| oktaaf |
2(5/53) |
2 |
2/1 =
2 |
2 |
Wanneer je naar de tellers van de breuken kijkt, dan zie je dat in deze
benadering een hele toon
soms 9 koma's is, soms 8. De toonaard van C wordt dan:
| toon |
do |
|
re |
|
mi |
|
fa |
|
sol |
|
la |
|
si |
|
do |
| aantal koma's |
|
9 |
|
8 |
|
5 |
|
9 |
|
9 |
|
8 |
|
5 |
|
| interval |
|
grote
hele
toon |
|
kleine
hele
toon |
|
halve
toon |
|
grote
hele
toon |
|
grote
hele
toon |
|
kleine
hele
toon |
|
halve
toon |
|
De reine tertsverhouding is kleiner dan een terts die afgeleid
wordt uit de stapeling van 4 kwinten.
Het verschil noemt men de syntonische komma (ongeveer 1/9 van een hele toon).
In dit systeem van 53-en wordt de syntonische komma opgevangen door de Turkse
koma.
Ze is nu geen afwijking meer, maar valt samen met het systeem van verdeling.
De hele toon tussen secunde (re) en terts (mi) wordt iets kleiner genomen.
Hetzelfde gebeurt met de si: als kwint van de reine terts is ze kleiner dan uit
stapeling van 5 kwinten.
In ons systeem maakt een perfect reine stemming het onmogelijk om te veranderen
van toonaard.
De verdeling met grote en kleine hele tonen blijft in andere toonaarden en wordt
opgevangen door de voortekening
aan de sleutel die aangeeft welke tonen verhoogt of verlaagd moeten worden.
Een verlaagde halve toon is hierbij niet gelijk aan een verhoogde toon, en dat
komt overeen met onze reine stemming.
In ons systeem komt een hele toon overeen met 9 komma's.
Een verhoging bedraagt 5 komma's, maar ook een verlaging bedraagt 5 komma's.
Dit verschil tussen b.v. een sol# en een lab hebben wij laten varen bij het toepassen
van een gelijkzwevende stemming.
Turkse muzikanten kunnen deze Turkse koma verschil laten horen.
Op een viool wordt de vinger een klein stukje verschoven, op de ney-fluit
bestaan zijn er aangepaste vingerzettingen.
Voor de wijzigingen van een komma bestaan aangepaste wijzigingsteken, zoals onze
mollen en kruisen.
Het Turks systeem kent verschillende toonaardverdelingen.
Naast de verdeling die hierboven beschreven wordt, bestaat er ook een verdeling
waar alle hele tonen wel gelijk zijn.
De oktaafverdeling gebeurt dan in stappen van 9 - 9 - 4 - 9 - 9 - 9 - 4 koma's.
Net zoals in ons systeem wijkt deze stemming in terts en septiem iets meer af
van de reine stemming.
Maar ook hier kan het verschil tussen sol# en lab gespeeld worden.
Octaafverdeling in cents
rekenen met machten
Rekenen met breuken en verhoudingen is niet zo handig.
De gelijkzwevende stemming laat een veel handigere manier van rekenen toe.
Alle toontrappen zijn te schrijven als machten van 2.
Voor het rekenen met machten weten dat a2 . a3 = a2+3
= a5 en a7 : a2 = a7-2 = a5.
Vermenigvuldigen komt neer op het optellen van de exponenten, delen op aftrekken
van de exponenten.
stapelen van kwinten
Een kwintverhouding is gelijk aan 2(7/12)
Een stapeling van twee kwinten heeft een verhouding van 2(7/12) . 2(7/12)
= 2(7+7)/12 = 2(14/12)
Een stapeling van vier kwinten heeft een verhouding van 2(7/12) . 2(7/12)
. 2(7/12) . 2(7/12) = 2(7+7+7+7)/12
Optellen en aftrekken van het aantal twaalfden is veel gemakkelijker om te
rekenen.
Voor elke toonafstand moeten we gewoon zeggen over hoeveel 12-en het gaat.
Voor tussenliggende tonen is het bovendien handiger om komma's te vermijden en daarom te
in 100sten te rekenen.
verhoudingen in een gelijkzwevende stemming
Elke halve toonsafstand komt overeen met 2(1/12)
of 100 cents.
secunde = 200 cents
terts = 400 cents
kwart = 600 cents
kwint = 700 cents
sext = 900 cents
septiem = 1100 cents
Een octaaf wordt dan 1200 cents.
Op deze manier kunnen we i.p.v. met machten en wortels van breukverhoudingen terug lineair
werken.
Verhogen wordt niet meer breuken vermenigvuldigen maar cents bijtellen.
Een verschil van 8 cents t.o.v. een toon is bovendien voor elke toon even groot.
Zo kunnen we afwijkingen op welke toonhoogte
ook beter vergelijken.
30 Hz verschil is meer t.o.v. 440 Hz dan 30 Hz t.o.v. 880 Hz.
Maar 10 cent t.o.v. een secunde is even veel als t.o.v. een septiem.
De verdeling in cents wordt ook toegepast op stemapparaatjes.
hoe omzetten van willekeurige verhoudingen naar
cents
Het omgekeerde van een macht noemt men wiskundig 'logaritme'.
'De hoeveelste macht van 2' schrijven we als 2log.
Een gelijkzwevende kwint, de 7e stap op 12 halve tonen is gelijk aan 700 cents.
Een reine kwint, de n-de stap op 12 halve tonen in een octaaf heeft als verhouding 3/2.
n/12 is dus de macht waartoe we 2 moeten verheffen om op 3/2 uit te komen.
Wiskundig zeggen we: n/12 = 2log (3/2).
Hieruit vinden we: n = 12 . 2log (3/2).
In cents uitgedrukt is een reine kwint gelijk is aan n = 1200 . 2log
(3/2).
2-logaritmen staan niet op een rekenapparaatje maar je kan ze uitrekenen met een
kleine omweg.
Volgens rekenregels van logaritmen is 2log(a) = log(a) : log(2)
Een reine kwintverhouding is dus gelijk aan 1200 . 2log(3/2)
= 1200 . log(3/2) : log(2) = 702 cents.
hoe omzetten van een afwijking in cents naar een
frequentie in Hz
Toonafstanden bereken je als een macht van 2.
In de gelijkzwevende stemming is de exponent van deze macht een breuk met noemer
12.
De afwijking in cents vul je in als de teller van deze exponent, de noemer wordt
1200 i.p.v. 12.
Een toon die 10 cent hoger is dan een toon van 440 Hz heeft een frequentie van
440 . 2(10/1200)= 442,55 Hz.
Deze berekening kan je ook met negatieve afwijkingen maken.
Een toon die 10 cent hoger is dan een toon van 440 Hz heeft een frequentie van
440 . 2(-10/1200)= 437,47 Hz.
verhoudingen voor de reine
intervallen
We kunnen nu elke frequentieverhouding omrekenen naar cents en
vergelijken met de gelijkzwevende stemming
met volgende formule:
toonafstand
tussentwee tonen in cents is gelijk aan
n = 1200: log(2) . log(frequentieverhouding van beide tonen)
met 1200: log(2) = 3983,3 kan je de formule ook schrijven als
n = 3986,3 . log(frequentieverhouding van beide tonen) |
|
stemming |
prime |
secunde |
terts |
kwart |
kwint |
sext |
septiem |
octaaf |
| rein |
0 |
204 |
386 |
498 |
702 |
884 |
1088 |
1200 |
|
gelijkzwevend |
0 |
200 |
400 |
500 |
700 |
900 |
1100 |
1200 |
In volgende bestanden kan je verschillende berekeningen uitvoeren:
gelijkzwevende stemming extra
De gelijkzwevende stemming is geen
wondertruc die alle problemen van stemmen en stemmingen oplost.
Er duiken zelfs heel wat problemen op.
melodisch denken en psychologie van uitvoerder
en luisteraar
Een mens denkt niet gelijkzwevend. Een pianist is gebonden aan de
stemming van zijn piano, maar zangers
en violisten niet.
Nauwkeurige metingen van opnames van beroemde uitvoerders tonen aan dat
ze in bepaalde
intervallen duidelijk afwijken
van de theoretische toon binnen een gelijkzwevende stemming, zonder dat
de toehoorder
een 'valse' toon waarneemt.
Strijkkwartetten, blokfluit- en gambaconsorts zoeken reine verhoudingen
op.
Reeds in zijn boek 'Harmonics or the Philosophy of musical Sounds' uit
1749 schrijft de Engelse wiskundige en
astronoom Robert Smith na heel wat berekeningen en uitweidingen over
stemmingen en toonaarden doodleuk:
"The
several parts of a concert wel performed upon perfect instruments do not
move exactly by the given intervals of
any system whatever, but only pretty nearly, and so as to make
perfect harmony as near as possible...
Now the reason why the best performers acquire a habbit of
making perfect harmony as near as possible is plainly this.
When the harmony is made perfectly they are pleased and
satisfied."
Je vindt het hele boek in facsimile online op
Harmonics - Robert Smith
Bovenstaand fragment en verdere uitwijdingen
over de muziekpraktijk vind je pag. 225 e.v.
M.a.w. een goede muzikant speelt met zijn oren en niet volgens
ingewikkelde temperingen en formules.
Voila, van relativeringsvermogen gesproken...
Smith doet er zelfs nog een schepje bovenop met de raad "nooit gezongen
partijen mee te spelen met het orgel,
tenzij om een 'imperfecte' zanger te begeleiden en hem zo er van te
behoeden om nog slechtere samenklanken te zingen
dan het orgel zelf speelt."
Er is in de muziekpraktijk geen onomstotelijk vastliggende dogma voor
een juiste intonatie en het menselijk oor vraagt het niet.
Tot er moet samengespeeld worden met een piano natuurlijk...
Geen wonder dat Beethoven de gelijkzwevende stemming helemaal niet zag
zitten en Maurice Ravel ronduit zei dat een
viool en een piano niet konden samenspelen.
waargenomen boventonen verschillen van theoretisch
model
Een theoretisch wiskundig model is een, in de praktijk duiken
voortdurend randvoorwaarden op.
Geef een speelgoedautootje een zetje, zodat het begint te rollen.
De theorie zegt dat, wanneer er geen kracht wordt op uitgeoefend, het
zal blijven voortrollen aan dezelfde snelheid.
Maar door de wrijving van de wieltjes en de rolweerstand met vloer of
tafel, zal het niet ver bollen.
En begin die weerstanden maar eens te berekenen...
Zo is het ook met snaren. Een snaar heeft materie. Bij het strijken of
plukken van een snaar wordt ze uitgerekt.
De vervorming roept een weerstand op in het materiaal en die stijfheid
van een snaar heeft als gevolg dat de waargenomen
boventonen hoger klinken dan de berekende tonen in het theoretisch
harmonisch model.
De afwijkingen nemen bovendien toe naarmate je verder gaat in de rij van
harmonische tonen. M.a.w. hoe hoger de boventoon
hoe groter de afwijking. Deze boventonen veroorzaken een conflict met de
tonen in de verst van het midden verwijderde octaven
van een piano.
psychoakoestiek
De psychoakoestiek onderzoekt hoe tonen worden
waargenomen.
Het blijkt duidelijk dat hogere tonen als lager worden waargenomen dan
hun reële toonhoogte.
De toonhoogte van een (zuivere) toon kan ook geschat worden. De
resulterende toonhoogteschaal heet de mel-schaal.
Het verband tussen toonhoogte (mel) en frequentie (Hz) dat men zo krijgt
is afgebeeld in onderstaande figuur.
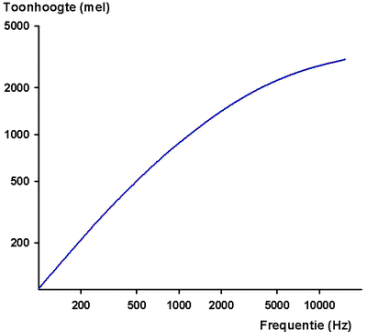
Voor frequenties onder de 1000 Hz lopen toonhoogte (in mels) en
frequentie (in Hz) gelijk. De helling van
de grafiek = 1.
Rond de 1000 Hz treedt een overgang op naar een logaritmisch verband.
Dit betekent dat de toonhoogte, uitgedrukt in mels,
steeds minder gaat toenemen wanneer de frequentie toeneemt.
Het verschijnsel is hoorbaar bij de hoogste octaven van een piano.
Het plaatje is eigenlijk nog ingewikkelder, omdat de subjectieve
toonhoogte ook afhangt van de luidheid van de toon.
Een toon van 1000 Hz behoudt zijn subjectieve hoogte, onafhankelijk van
de luidheid.
Maar voor lage tonen geldt: hoe luider hoe lager, voor hoge tonen hoe
luider hoe hoger de subjectieve toonhoogte.
Bovendien is de relatie tussen luidheid en toonhoogte anders voor
sinustonen dan voor complexere (harmonische) tonen...
Een bijkomend psychoakoestisch verschijnsel dat we kwijtraakten met de
gelijkzwevende stemming zijn de verschiltonen,
waarbij we bij harmonisch samenklinkende tonen een derde toon lijken te
horen, met als frequentie het verschil van de
frequenties. Voorbeeld: een la (440 Hz) en een mi (660 Hz) brengen een
verschiltoon voort van 220 Hz.
Dit toon wordt niet gespeeld, het zijn onze hersenen die deze bijkomende
toon produceren.
Maar wanneer je harmonische tonen opgeeft om het toonsysteem eenvoudiger
te maken, verlies je dit fenomeen.
Luister maar eens naar een gamba consort dat in reine stemming
renaissance muziek speelt ...
M.a.w. Geluidswaarneming wordt niet alleen bepaald door wat muzikanten
echt spelen.
Ook onze oren en onze hersenen spelen een belangrijke rol.
kwinten in hoogste octaven
Dat reine kwinten en reine octaven niet samen gaan, dat wist je al.
Voor een la met een frequentie van 440 Hz is de gelijkzwevende stemming
geen probleem.
Een reine kwint van deze toon heeft een frequentie van 440 . 3/2 =
660 Hz.
Een gelijkzwevende kwint van deze toon heeft een frequentie van 440 . 2(7/12)
=
659.3 Hz.
Dit verschil van 0.7 Hz is niet waarneembaar door het menselijk oor.
Het waarneembare verschil tussen toonhoogten (= de frequentieresolutie)
bedraagt ongeveer 2 Hz.
Maar elk octaaf hoger zal dit verschil verdubbelen.
Je merkt dat
het verschil tussen de reine en de gelijkzwevende kwint al snel merkbaar
wordt.
| la |
. 3/2
|
. 2(7/12) |
verschil |
440 Hz
880 Hz
1760 Hz
3520 Hz |
660 Hz
1320 Hz
2640 Hz
5280 Hz |
659.3 Hz
1318.5 Hz
2637 Hz
5274 Hz |
0.7 Hz
1.5 Hz
3 Hz
6 Hz |
een pianostemmer moet oren hebben
Heb je geen ervaring in het stemmen van een piano probeer je het zelf
een eenvoudig stemapparaatje, dan zal het resultaat
pover zijn, ook al is er niets mis met het apparaatje.
Het probleem is het verschil tussen het theoretisch model van de
gelijkzwevende stemming zelf en de praktijk.
Hogere tonen klinken te laag, boventonen klinken te hoog en
gelijkzwevende kwinten komen te laag uit...
Een pianostemmer gaat daarom de uiterste octaven van het pianoklavier
lichtjes uitrekken.
De hoogste tonen wordt hoger gestemd dan in het theoretische model, de
laagste lager.
De stijfheid van snaren is materiaaleigen. Ze is ook belangrijker in
kortere piano's dan in langere.
En ook de psychoakoestiek laat zich niet zomaar vertalen in vaststaande
formules.
We kunnen wel berekenen hoeveel groter je een octaaf moet maken om een
kwint rein te maken.
De vergelijking wordt:
x7/12 = 1.5
De oplossing is
x = 1.512/7 =
2.0039
Pas je dit bv. toe op een la van 1760 Hz, dan wordt het octaaf 1760 .
2.0039 =
3526.8 Hz i.p.v. 3520 Hz.
De kwint van een la 1760 Hz wordt nu wel perfect rein.
De net iets hoger gestemde tonen klinken ook aangenamer en briljanter.
Een pianostemmer moet niet alleen een pianosleutel hebben en een
stemapparaat, maar vooral oren.
Niet alleen Pythagoras stuitte op de grenzen van een mooi theoretisch
model...
Ook het wiskundig model van de gelijkzwevende stemming heeft zijn
grenzen.
Pianofabricant Steinway heeft zijn topstemmers, concerthuizen laten niet
de eerste de beste stemmer komen.
Sommige concertpianisten zweren bij een vaste stemmer, terwijl de Franse
toppianist Alexandre Tharaud zelfs
geen piano heeft staan. Hij oefent bij vrienden om zich
niet te fixeren op het geluid van één piano op één plaats.



