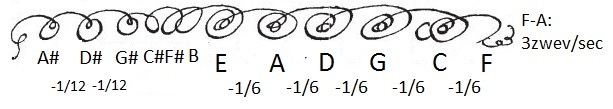barokstemmingen
wiskunde-interactief.be
Het geheel rond sinusfuncties, geluid en
muziek is uitgewerkt op acht pagina's:
-
van
sinusfuncties tot een toonsysteem schetst
de natuurkundige en wiskundige basis van geluid.
-
samenklanken
en verhoudingen beluistert en onderzoekt
het resultaat van samenklinkende geluiden.
-
boventonen
en zwevingen onderzoekt
het voorkomen van natuurlijke boventonen en het
waarnemen
van zwevingenbij tonen die nauwelijks van elkaar verschillen.
-
de kwinten
van Pythagoras ontleedt hoe Pythagoras
vanuit kwintverhoudingen een toonladder opbouwt.
-
het komma
van Pythagoras' ontleedt hoe Pythagoras
vanuit kwintverhoudingen een toonladder opbouwt.
-
een
muzikale zoektocht' volgt de
muziekgeschiedenis in zijn zoektocht naar
welluidendheid.
- barokstemmingen'
ontleedt enkele pogingen om nieuwe oplossingen
te vinden voor nieuwe muzikale wensen.
-
de
kettingbreuk van Huygens' ontleedt Huygens'
berekeningen om een 'juister' klinkende
toonladder uit te bouwen.
Extra: partituurfragmenten en youtube-filmpjes
illustreren de theorie.
-
de zoektocht in klank en beeld:
opmerking over het afspelen
van geluid:
GeoGebra is in de eerste plaats een fantastisch
wiskundeprogramma maar geen gesofisticeerd
keyboard.
Verschijnt er bijvoorbeeld in een grijs scherm
een foutmelding over het afspelen, herlaad dan
gewoon de pagina en
klik gewoon opnieuw op 'speel'. Doe hetzelfde
wanneer je het afspelen van een geluid niet kan
stoppen.
Hoor je geen geluid, probeer dan eens een andere
browser...
Zelfs met deze gebreken is het een unieke manier
voor wiskundigen om iets over muziek te leren en
omgekeerd. |
Muziekwetenschappers en wiskundigen zoeken oplossingen voor de problemen die
zich stellen
met de stemming van Pythagoras en de reine stemming.
We verlopen nog een keer de problemen en verkennen enkele oplossingen die
uitgewerkt werden door
Rameau, Werckmeister, Kirnberger en Valotti.
De meesten van hen werkten meer dan een voorstel uit.
De uitwerking van Werckmeister is eigenlijk Werckmeister III (van 6
uitwerkingen) en Kirnberger is Kirnberger III.
Stemming van Pythagoras en de reine stemming
| uitgangspunt |
Tonen verhouden zich
als gehele getallen |
| realisatie |
Alle afstanden worden
opgebouwd vanuit de reine kwintverhouding 3/2 |
| probleem |
Kwinten sluiten niet
aan op oktaven en tertsen.
Een terts die opgebouwd is vanuit een kwint is niet rein en klinkt te
hoog. |
| muziek |
- veel samenklanken
van kwinten.
- tertsen worden vermeden |
In de reine stemming wordt de kwintafhankelijkheid van de terts opgegeven.
| uitgangspunt |
De
kwintafhankelijkheid van de terts opgegeven. |
| realisatie |
Secunde en kwart worden
opgebouwd vanuit de reine kwintverhouding 3/2.
De terts krijgt de reine verhouding 5/4.
Sext en septime worden opgebouwd vanuit de terts. |
| probleem |
Een toonladder
bestaat uit grote en kleine halve tonen. |
| muziek |
Een muziekstuk staat in
de
toonaard waarin het instrument rein gestemd is. |
De afstand do - re is een grote hele toon met verhouding 9/8.
De afstand re - mi is een kleine hele toon met verhouding 10/9.
De verhouding tussen beide noemen we het syntonische komma = 81/80.
Middentoonstemming
Door de kwintafhankelijk van tertsen op te geven werden de
tertsen wel terug rein,
maar sloot men zich op in een toonaard.
Een grotere vrijheid tussen toonaarden is slechts mogelijk met tertsen, bepaald
door de kwint.
De enige mogelijkheid om tertsen terug rein(er) te krijgen is dus de kwint te
verkleinen.
Dit noemt men temperen.
De middentoonstemming verlaagt de kwint met 1/4 van een komma.
- Met het komma bedoelen we het syntonisch komma 81/80
- 1/4 van dit komma bereken je als 4√(81/80)
- De kwint verlagen met 1/4e komma bereken je als 3/2 : 4√(81/80)
De kwintverhouding wordt daarmee 3/2 : 4√(81/80)
= 3/2 : 4√(34/24.5)
= 3/2 : 3/2 . 4√5 =
4√5 =
1,49535
Dit is wiskundig mooi gevonden, want de tertsverhouding komt nu perfect uit op
5/4:
De terts verhouding is gelijk aan 4 kwinten : 2 oktaven = 4√5
x 4√5 x 4√5 x 4√5 :4 = (4√5)4
: 4 = 5 : 4.
Resultaat:
- De terts is perfect rein.
- De kwint is iets te klein maar wijkt nauwelijks af van de 3/2 verhouding.
- Alle afstanden kunnen berekend worden vanuit de kwint.
- De afstanden C-D en D-E zijn even groot en niet meer groot en klein zoals in
de reine stemming.
| uitgangspunt |
De tertsen moeten
afgeleid worden van de kwint en tegelijk rein
klinken. |
| realisatie |
De kwintverhouding 3/2
wordt verkleind met 1/4e komma tot 4√5 =
1,49535
|
| probleem |
De kwintencirkel
sluit zeer slecht. De sluitende kwint is veel te
groot.
Ze wordt wolfskwint genoemd en moet vermeden worden. |
| muziek |
Het vermijden van
wolfskwint beperkt nog de onafhankelijkheid van
toonaarden. |
Ongelijkzwevende stemmingen
Alle tertsen rein maken door de kwinten te verkleinen tot de middentoonskwint is
niet te verzoenen met een vrijheid
van toonaarden. Omdat in de barokmuziek die vraag naar meer harmonische vrijheid
groter wordt, moet ook hier
weer een compromis gezocht worden.
Dit compromis bestaat er in om het aantal verlaagde kwinten in de kwintencirkel
te beperken.
In de 17e en 18e ontwikkelen diverse componisten uiteenlopende stemmingen.
Omdat alle kwinten in de kwintencirkel niet meer gelijk zijn, zullen ook de
onderlinge verhoudingen tussen de
verschillende toontrappen in verschillende toonaarden niet meer gelijk zijn.
Je kunt dus niet zeggen: "zo klikt deze stemming", maar wel "zo klinkt deze
toonaard in deze stemming."
Het uitgangspunt van elke poging is wel steeds hetzelfde:
- zo rein mogelijke tertsen in de meest gebruikte toonaarden
- een zo goed mogelijk aansluitende kwintencirkel om in zo veel mogelijk
toonaarden te kunnen spelen.
Jean Philippe Rameau (1683 - 1764)
| uitgangspunt |
- zoveel mogelijk
reine tertsen in de centrale toonaarden van de
kwintencirkel
- vermijden van de wolfskwint door niet alle kwinten te temperen. |
| realisatie |
- 7
middentoonskwinten en 3 reine kwinten
- twee licht overmatige kwinten om de kwintencirkel te sluiten |
| resultaat |
Er zijn 4 reine
tertsen.
De verhoudingen binnen de centrale toonaarden en de toonaarden die het
verst verwijderd zijn van de C verschillen aanzienlijk. |
| verhoudingen van
de tertsen in: |
| Bb, F, C en G: |
5/4 |
= 1,25 |
| D: |
(4√5)3
. 3/2 : 4 |
= 1,2539 |
| A: |
(4√5)2
. (3/2)2 : 4 |
= 1,2578 |
| E: |
4√5 . (3/2)3
: 4 |
= 1,2617 |
Andreas Werckmeister (1645 - 1706)
| uitgangspunt |
-
tertsen van centrale toonaarden zo rein mogelijk
- het verschil tussen de toonaarden verkleinen |
| realisatie |
4 middentoonskwinten in de kwintencirkel, maar
niet aaneensluitend.
|
| resultaat |
Geen enkele terts is
helemaal klein, maar de meeste bijna.
Verschillen tussen de toonaarden zijn kleiner. |
| verhoudingen van
de tertsen in: |
| C en F: |
(4√5)3
. 3/2 : 4 |
= 1,2539 |
| D, G en Bb: |
(4√5)2
. (3/2)2 : 4 |
= 1,2578 |
| A, Eb,E en B: |
(4√5)2
. (3/2)3 : 4 |
= 1,2617 |
Johann Kirnberger (1721 - 1783)
| uitgangspunt |
De kwintencirkel zo
goed mogelijk laten aansluiten. |
| realisatie |
4 aaneensluitende middentoonskwinten worden aangevuld met een
wat
verderop geplaatste gelijkzwevende kwint.
|
| resultaat |
De terts is rein op C
en bijna rein op aansluitende toonaarden
De kwintencirkel sluit zo goed als perfect aan. |
| verhoudingen van
de tertsen in: |
| C: |
5/4 |
= 1,25 |
| F en G: |
(4√5)3
. 3/2 : 4 |
= 1,2539 |
| D en Bb: |
(4√5)2
. (3/2)2 : 4 |
= 1,2578 |
| A: |
4√5 . (3/2)2
. 2(7/12) : 4 |
= 1,2603 |
| E: |
(3/2)4 . 2(7/12)
: 4 |
= 1,2642 |
Francesco Antonio Vallotti ( 1697 - 1780)
| uitgangspunt |
verschillen tussen de
toonaarden verkleinen door de kwint minder te
temperen. |
| realisatie |
De kwintverhouding 3/2
wordt slechts verkleind met 1/6e komma tot
3/2 : 6√(81/80)=
1,4969
|
| resultaat |
Geen enkele terts is
helemaal rein.
De 1/6e komma verkleinde kwint ligt dichter bij de reine kwint dan de middentoonskwint.
De verschillen tussen de toonaarden zijn beperkt.
|
| verhoudingen van
de tertsen met V= 1,4983 in: |
| F, C en G: |
V4 : 4 |
= 1,255 |
| Bb en D: |
V3 . 3/2 : 4 |
= 1,2578 |
| Eb en A: |
V2 . (3/2)2
: 4 |
= 1,2604 |
| E: |
V . (3/2)3 : 4 |
= 1,2630 |
| B: |
(3/2)4 : 4 |
= 1,2756 |
Vallotti verlaagt de kwint met 1/6 van een komma.
- Met het komma bedoelen we het syntonisch komma 81/80
- 1/6 van dit komma bereken je als 6√(81/80)
- De kwint verlagen met 1/6e komma bereken je als 3/2 : 6√(81/80)
De kwintverhouding wordt daarmee 3/2 : 6√(81/80)
= 1,4969
Vergelijking
We kunnen de afwijkingen t.o.v. de gelijkzwevende stemming het best vergelijken
door ze uit te drukken in cent.
100 cent komt hierbij overeen met een halve toon in de gelijkzwevende stemming.
In volgende tabel lees je de waarden af voor twee toonaarden.
We starten in het centrum van de kwintencirkel met de toonaard in C (do groot).
|
toonaard C t.o.v. gelijkzwevend |
secunde |
terts |
kwart |
kwint |
sext |
septime |
| rein |
+8 |
-14 |
-2 |
+2 |
-16 |
-12 |
| middentoonstemming |
-7 |
-14 |
+2 |
-3 |
-10 |
-17 |
| Rameau |
-7 |
-14 |
+2 |
-3 |
-10 |
-17 |
| Werckmeister |
-7 |
-9 |
+2 |
-3 |
0 |
-6 |
| Kirnberger |
-7 |
-14 |
+2 |
-3 |
-10 |
-12 |
| Valotti |
-4 |
-7 |
+2 |
-2 |
-5 |
-8 |
Opvallend is dat de gelijkzwevende terts die we kennen veel hoger is dan in al
de barokstemmingen.
Dit komt omdat gekozen wordt voor reine tertsen, die kleiner zijn dan in onze
gelijkzwevende stemming.
Werckmeister en Vallotti kiezen voor iets minder reine tertsen om gemiddeld
beter te scoren
over het geheel van de toonaarden. Ze gaan meer in de richting van een
gelijkzwevende stemming.
|
toonaard E t.o.v. gelijkzwevend |
secunde |
terts |
kwart |
kwint |
sext |
septime |
| rein |
+8 |
-14 |
-2 |
+2 |
-16 |
-12 |
| middentoonstemming |
-7 |
-14 |
+2 |
-3 |
-10 |
-17 |
| Rameau |
-1 |
+3 |
+2 |
-3 |
0 |
+4 |
| Werckmeister |
-1 |
+3 |
+2 |
+2 |
0 |
+4 |
| Kirnberger |
+4 |
+6 |
+3 |
+2 |
+4 |
+8 |
| Valotti |
+1 |
+4 |
+2 |
-2 |
+2 |
+6 |
De toonaard E (mi groot) is in de kwintencirkel 4 stappen verwijderd van C.
De verschillen tussen de stemmingen vallen nu meer op, zeker in de tertsen.
Vallotti blijft ook hier heel dicht bij de gelijkzwevende stemming.
Het verschil tussen de afwijkingen in de toonaarden C en E is bij hem ook veruit
het kleinst.
stemmingen en muziek
In de stemming 1/6e komma getemperde stemming van Vallotti zijn de onderlinge verschillen het kleinst.
De optie 'de absolute reine toon opgeven ten voordele van
kleinere verschillen' gaat dan ook het meest in
de richting van een gelijkzwevende stemming,
waarbij de verschillen gelijkmatig verdeeld worden over alle tonen.
Reine tonen worden opgegeven ten voordele van de
flexibiliteit tussen toonladders.
In de 19e eeuw evolueert men geleidelijk in de richting van een gelijkzwevende
stemming.
Zo wordt de opbouw van een symfonie steeds comlexer.
Beethoven en Mahler kunnen een hele evolutie opbouwen waarin ze meerdere keren van toonaard veranderen.
Schubert kan in zijn liederen strofen in een grote
tertstoonladder afwisselen met een strofe in
kleine terts
en in onze populaire muziek kan een laatste refrein zonder probleem een halve
toon hoger klinken dan de vorige keren.
Dat tertsen en kwinten nu niet meer helemaal zuiver klinken
wordt ook minder een probleem.
Het klavecimbel, dat rijk is aan boventonen, heeft zijn rol
als klavierinstrument moeten afstaan aan de piano.
De piano is arm aan boventonen, zodat niet-helemaal
rein klinkende tonen veel minder storen.
Inmiddels zijn we er zo gewoon aan dat we
zelfs verbaasd opkijken wanneer we voor het eerst vernemen dat een
'goed' gestemde piano
eigenlijk vals staat...
Misschien wordt het nu ook duidelijk dat 'Oude Muziek' spelen op historische
instrumenten meer is dan nostalgie.
Renaissance- en barokmuziek steunt veel meer op de klankwereld van reine
verhoudingen.
Daarom klinkt een blokfluitkwartet ook verrassend orkestraal een groot.
Componisten componeren in de klankwereld die ze kennen.
Die 'grote' klankwereld hebben we verlaten voor een vlakkere, uniforme klank
waarbij we ons vrij en virtuoos kunnen
bewegen doorheen alle toonaarden.
Bach op klavecimbel en Mozart op pianoforte en Beethoven op een 19e eeuwse piano klinken
dan ook anders
dan
op een moderne, gelijkzwevend gestemde Steinway-vleugel.
Een organist die op historische orgels speelt, let er op welke muziek hij op
welk instrument we of niet speelt.
Een blokfluitensemble heeft niet zonder reden zoveel verschillende instrumenten
bij.
En misschien begrijp je nu waarom Ravel vond dat een viool en een piano niet
samenklinken.
Een viool heeft de neiging om reine intervallen te spelen maar onze vleugel
volgt haar daarin niet...
Bachs 'Das Wohltemperierte Klavier'
Wanneer we spreken over het spelen in verschillende toonaarden, kunnen we niet
om Johann Sebastian Bach.
Hij componeerde in 1722 een reeks van preludes en fuga's in elk van de 24
mogelijke toonaarden
"ter gebruik door en ten bate van leergierige jongeren en als tijdverdrijf voor de
geoefende muzikant".
Twintig jaar later, in 1742, schreef hij nog een tweede bundel. De twee bundels
kennen we nu als een werk.
'Welgetemperd' betekent dat er geen intervallen voorkomen die
absoluut moeten vermeden worden.
Op die manier werd het effectief mogelijk in elke mogelijke toonaard te spelen.
Er is al veel geschreven over de stemming die Bach hiervoor zelf gebruikte.
Vast staat dat Welgetemperd iets heel anders is dan de gelijkzwevende stemming
die wij gebruiken.
Gelijkzwevend betekent dat het komma van Pythagoras gelijkmatig verdeeld wordt
over elk van de 12 halve tonen.
In 'welgetemperde' stemmingen als Werckmeister III en Kirnberger worden ze
ongelijk verdeeld.
Hierbij klinken de centrale toonaarden in de kwintencirkel zo rein mogelijk.
De verder
verwijderde klinken 'aanvaardbaar'.
Voor Bach wordt hierbij vaak verwezen naar Werckmeister III.
In 2005 publiceerde Bradley Lehman een opmerkelijke theorie.
Bach zou op de titelpagina van zijn werk zelf een aanduiding getekend hebben
over de stemming.

Nu zijn krulletjes niet ongewoon in geschriften van die tijd, maar Lehman
plaatste er cijfers bij:
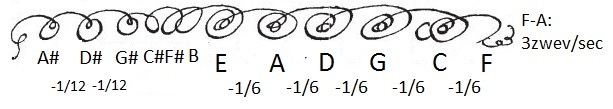
Elk krul staat voor een opeenvolgende kwint. De C van 'klavier' geeft de C
(do) aan.
Een krul met een extra rondje staat voor een tempering met 1/12e komma van Pythagoras.
Een krul met twee rondjes staat dus voor een tempering met 2/12e komma of 1/6 komma van Pythagoras.
Als stemhulp zouden de 3 rechtse krulletjes staan voor 3 zwevingen per seconde
tussen F en A.
Ter herinnering: 12 kwinten komen net iets
hoger uit dan 8 octaven.
De verhouding 12 kwinten/7 octaven =
531441/524288 of 1,0136
Om de kwintencirkel te sluiten, moet dit komma
verdeeld worden over een aantal van de 12 halve
tonen.
In een kwintencirkel kan je zien hoe de puzzel
klopt:
Bach verdeelt het komma in 5 maal 1/6 komma en 2
maal 1/12 komma. |

De grootste afwijking in heel de kwintencirkel is 1/6 van een komma van
Pythagoras:
| uitgangspunt |
Alle mogelijke
toonaarden speelbaar maken. |
| realisatie |
Het komma van
Pythagoras wordt verdeeld over een aantal
kwinten.
|
| resultaat |
Zelfs voor de
verst verwijderde kwinten klinken zowel kwinten
als tertsen erg goed.
|
| verhoudingen van
de tertsen |
| F, C : |
(-1/6 PC)4 : 4 |
= 1,2542 |
| Bb: |
(3/2) . (-1/6 PC)3 : 4 |
= 1,2570 |
| Eb: |
(-1/12 PC) . (3/2)
. (-1/6 PC)2 : 4 |
= 1,2585 |
| D: |
(-1/6 PC)2 . (3/2)2
: 4 |
= 1,2599 |
| A: |
(-1/6 PC) . (3/2)3
: 4 |
= 1,2628 |
| E: |
(3/2)3
. (-1/12 PC) .
: 4 |
= 1,2649 |