boventonen en zwevingen wiskunde-interactief.be

Boventonen
Instrumenten produceren geen zuivere sinusfuncties. Steeds klinken zogenaamde harmonische tonen of boventonen mee.
Hoeveel en in welke mate, bepaalt de kleur van de toon. Dit wordt nagebootst in elektronische piano’s.

Ook in GeoGebra kunnen we geluid kleuren door de som van verschillende sinusfuncties te laten horen en het gewicht
van de termen te veranderen.

Wanneer een pijpen van het orgel wordt aangeblazen, ontstaat geluid van diverse golflengtes. 
Maar alleen het geluid met een golflengte die past in de lengte die ter beschikking staat ( orgelpijp, fluit, snaar…),
kan blijven bestaan. De meest eenvoudige golf bepaalt de toonhoogte. 
De andere tonen hoor je niet als aparte tonen maar als een integrerend deel van de grondtoon.  In het geval van een
gesloten pijp treedt er een staande golf op als de halve golflengte gelijk is aan de lengte van de pijp.
Hoe langer de pijp, hoe langer de golf en hoe kleiner de frequentie:
Langere orgelpijpen produceren lagere tonen dan kortere.  

Maar er is niet alleen die ene golf.
Ook golven waarbij de golflengte 'past' bij de lengte van de pijp kunnen een staande golf
veroorzaken, zoals golflengten van 1x de lengte van de pijp, 2x de lengte van de pijp, etc. 

geluidssnelheid = frequentie . golflengte  of in formulevorm: v = f . l 
Met een geluidssnelheid van ca. 343 m/sec kan je de lengte van een orgelpijp berekenen voor een willekeurige frequentie.
Wat zijn nu de frequentieverhoudingen van deze boventonen? We weten hierbij:

een verhouding 2/1 bepaalt een octaaf (do - do)
een verhouding 3/2 bepaalt een kwint (do - sol)
een verhouding 5/4 bepaalt een grote terts (do - mi)

delen door    2 3 4 5 6

verhouding    2/1   3/2 4/1 5/4 6/4 = 3/2

toontrap      octaaf kwint van octaaf dubbel octaaf grote terts van dubbel octaaf kwint van dubbel octaaf

toon    do sol do mi sol

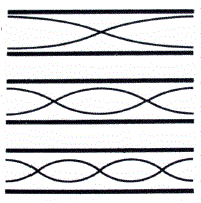Pijpen met open uiteinden De golf moet een buik vertonen. De mogelijke golflengtes zijn dezelfde als bij een gesloten pijp.

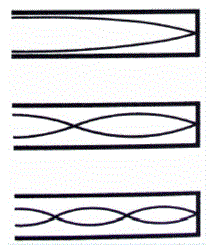Pijpen met een open en een gesloten uiteinde Aan het open uiteinde vertoont de golf een buik vertonen, aan het gesloten uiteinde een knoop. 1/4 van een volledige periode past nu in de pijp. Dat levert een toon op    die een octaaf lager is dan bij een volledig open of gesloten pijp met een zelfde lengte. Vervolgens passen respectievelijk 3/2, 5/2, 7/2 ... van een halve periode in de pijp. Enkel de oneven boventonen (3x, 5x, 7x de basisfrequentie) klinken dus.  Een pijp met een open en een gesloten uiteinde heeft daarom een heel andere    klankkleur dan een open of een gesloten pijp.Een voorbeeld hiervan is de klarinet.  Ook andere vormaanpassingen (rechte of conische vorm van de pijp) beinvloeden de boventonen en dat geeft elk instrument zijn typische kleur. Meer info vind je in gespecialiseerde lectuur of bv op volgende Engelstalige website How do Woodwind Instruments work

Boventonen bestaan dus vooral octaven en kwinten, die als welluidend ervaren worden.
Bij een verdere verdeling treden ook tonen op die niet zuiver klinken.
Zo kunnen verdelingen in 7,11, 13 of 14 niet herleid worden tot een harmonisch klinkende frequentieverhouding.
Bij het bouwen van instrumenten komt het er op aan om al experimenterend met de bouw
het relatief aandeel van deze storende tonen te verminderen en zo mogelijk uit te schakelen.

Zwevingen
Twee tonen die nauwelijks van elkaar verschillen ervaren we als heel onaangenaam.
Maar hoe ziet de grafiek van zo een trilling er uit?

Wanneer een la (220 Hz) samenklinkt met geluidstrilling van 216 hoor je een zweving.
Met de regels voor het optellen van sinussen, kan je de som schrijven als een functie met twee factoren:
- de sinusfactor is de snelle trilling met een frequentie van 218 Hz (het gemiddelde van de twee).
  Het is deze factor die de toonhoogte bepaalt, net iets lager dan de la van 220 Hz.
  Merkwaardig is dat je dus geen twee aparte tonen hoort, maar slechts één toon.
- Deze sinusgrafiek lijkt te trillen tussen de twee cosinusfuncties fg₁ en g₂ = - g₁.
  De functie g₁ vinden we terug als de cosinusfactor van de somfunctie.
  Ze heeft een veel grotere periode dan de sinusfunctie die de toonhoogte bepaalt.
  Deze factor speelt de rol van amplitude.
  De absolute waarde van de cosinusfactor neemt 4 keer per seconde de maximale waarde 2 aan.
  Omdat de amplitude van de toon die we horen verandert, horen we zwevingen in de toonsterkte.
  Het aantal zwevingen per seconde is gelijk aan het frequentieverschil.
  Hoe kleiner het verschil tussen de twee tonen, hoe trager dus deze zwevingen.
  Gitaarsnaren of orgelpijpen kan je stemmen door deze zwevingen weg te werken.

De amplitude van een geluidsgolf bepaalt de sterkte van het geluid.
Verschillen twee geluidsgolven lichtjes van frequentie, dan zullen de eerste golven elkaar nog versterken.
Als resultaat horen we een duidelijke sterke toon.
De toon met de laagste frequentie zal nu steeds meer achterlopen. De twee golven geraken uit fase.
Als resultaat horen we een toon die steeds minder sterk is.
Na verloop van tijd komen we aan een punt waar beide in tegenfase zijn. We horen dan geen geluid.
Omdat patroon zich blijft herhalen horen we een pulserend geluid.
Uiteraard bepaalt het frequentieverschil hoe dikwijls per seconde deze cyclus voorkomt.

Visueel kunnen we dit ook duidelijk maken door een strook waarin we verticale streepjes plaatsen.
We plaatsen nu twee verdelingen op elkaar, waarvan het aantal streepjes verschilt.
 
Wanneer het aantal streepjes in de tweede verdeling kleiner is dan in de eerste, dan zal het binnen de strook meerdere
keren gebeuren dat de streepjes van de tweede verdeling net samenvallen met de witte gaatjes in de eerste.
Je ziet een vlekachtige verdichting binnen het streepjespatroon.
Het aantal van deze verdichtingen binnen de strook hangt natuurlijk af van het verschil tussen het aantal streepjes.
Dit kan je vergelijken met het patroon van zwevingen dat je hoort bij geluidsgolven waarbij de frequentie licht
verschillend is. Per seconde gebeurt het meerdere keren dat de golven in fase en in tegenfase zijn.
Ook hier is het aantal zwevingen gelijk aan het verschil in frequentie.

combinatietonen
We nemen het fenomeen zwevingen maar waar wanneer het frequentieverschil beperkt is, ongeveer 10 Hz.
Daarboven horen is er eerst nog een zone waarin we (nog steeds) één toon horen, maar wel een heel onaangename.
Pas wanneer het verschil groter wordt, pakweg 20 Hz, horen we twee aparte tonen.
Wanneer het verschil groter wordt, doet zich een nieuw fenomeen voor: de verschiltoon.
Violist Giusepppe Tartini (1692-1770) ontdekte dat wanneer twee tonen in een harmonische verhouding samenklinken,
een derde toon worden waargenomen met als frequentie het verschil van de frequenties van de aparte tonen.
Voorbeeld: een la (440 Hz) en een mi (660 Hz) brengen een verschiltoon voort van 220 Hz (lagere la).
Het blijkt uit medisch onderzoek sommige combinatietonen gecreëerd worden door vervormingen van de geluidsgolven
in onze hersenen andere dan weer in het slakkenhuis van onze oren.
Deze tonen worden bv. gebruikt in het stemmen van blokfluiten, maar ook in de orgelbouw.
Heel laag klinkende orgelpijpen zijn erg duur om te maken en ook erg groot. Maar koppel je aan een orgelregister
een tweede register dat telkens de reine kwint van de gespeelde toon laat meeklinken, dan zal je de indruk hebben
dat een octaaf lager een basregister meeklinkt ook al zit dat niet in het orgel en wordt de toon niet gespeeld.

Naast verschiltonen bestaan er ook, zacht meeklinkende, somtonen.
Voorbeeld: een la (440 Hz) en een mi (660 Hz) brengen een somtoon voort van 1100 Hz (hogere do#).

Door deze psychoakoestische fenomenen klinken ensembles van blokfluiten of viola de gamba's zo 'groot', terwijl ze uit
eerder stille instrumenten bestaan. En dat effect verliezen we in een gelijkzwevende stemming.

Boventoonzingen
Anna Maria Hefele kan tijdens het zingen boventonen laten meeklinken.
Ze toont het in een filmpje op Youtube: