de kettingbreuk van Huygens wiskunde-interactief.be

31-tonensysteem
De varianten van Werckmeister en andere tijdgenoten op de middentoonstemming focussen sterk op zo rein
mogelijke toonverhoudingen. In deze stemmingen heeft elke toonaard een eigen kleur.
De afwijkingen ten opzichte van reine afstanden neemt de toe in verder afgelegen toonaarden van de kwintencirkel,
zodat de meest courante toonaarden zo zuiver mogelijk klinken.

Een tweede benadering is: "Kunnen we een oktaaf zo onderverdelen dat alle toontrappen gelijk zijn en tegelijk
rein (of toch minstens zo rein mogelijk) klinken?"
Net zoals in de tijd van Pyhtagoras zijn het ook nu wiskundigen en natuurkundigen die aan de kar trekken,
zoals de vader van Galileo Galilei, Simon Stevin, Christiaan Huygens, Descartes en Leonard Euler.
Hun benadering komt er op neer een oktaaf in zoveel stapjes onder te verdelen dat de kwint samenvalt
met een van die stapjes (en als het even kan ook de kwart en de terts).

Huygens gebruikt een kettingbreuk om de kwintverhouding ⁴√5  van de middentoonstemming  te noteren.



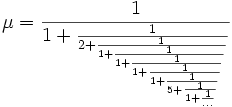
Breuk of decimaal getal als kettingbreuk
De gedachte achter de kettingbreuknotatie is dat een reëel getal de som is van een geheel getal en een getal tussen 0 en 1.
Dit deel kan geschreven worden als een breuk.
Deze breuk schrijven we als het omgekeerde van zijn omgekeerde: a/b = 1/(b/a).
Het uitwerken van b/a geeft weer een decimaal getal, enzovoort.
Zo ontstaat een kettingbreuk.
Op deze manier kan je bijvoorbeeld de breuk 17/5 schrijven als een kettingbreuk:

Ook een decimaal getal kan je schrijven als een kettingbreuk:




Kettingbreuk als gewone breuk
Omgekeerd kan je een kettingbreuk schrijven als een gewone breuk door van onder uit terug te rekenen:
 
Bij rationale getallen is het werken met kettingbreuken niet de snelste manier om de breuknotatie te vinden.
Het is wel een efficient middel om benaderingen in breukvorm te vinden voor irrationale getallen.
Een irrationaal getal kan je schrijven als een oneindige kettingbreuk.
Je vindt een benadering door de kettingbreuk ergens af te breken en terug te rekenen tot een gewone breuk.
Elke verdere stap levert een betere benadering op in breukvorm.
Bekend zijn kettingbreuken en breukbenaderingen voor pi. 




de middentoonkwintverhouding uitgewerkt als kettingbreuk
Even recapituleren:
- De reine kwintverhouding is 3/2 (=1,5) en de reine tertsverhouding is 5/4.
- Binnen een octaaf wordt een terts berekend door 4 kwinten op elkaar te stapelen en twee octaven terug te rekenen..
  Omdat de verhouding 3/2 echter iets te groot is, zal ook de terts te groot zijn en niet rein klinken.
- De middentoonstemming lost dit verschil op door te kwint iets kleiner te nemen:
  4 kleinere kwinten met verhouding ⁴√5 (= 1,4953) op elkaar stapelen geeft als resultaat:
  (⁴√5 )⁴ : 4 = 5/4 of een perfecte terts.
 
De wiskundige uitdaging van Huygens is nu:
"Kan je getallen p en q vinden, zodanig dat
wanneer je een octaaf in p stappen onderverdeelt,
je bij de q-e stap precies op deze middentoonverhouding ⁴√5 uitkomt? "

De frequentie verdubbelt per octaaf.
Neem je geen volledige octaafafstand, maar slechts q/p ervan, dan wordt de frequentie 2^(q/p).
Willen we dat we hierbij op de middentoonverhouding ⁴√5 uitkomen dan krijgen we:

Wat zijn we nu hiermee?
Wel: wanneer we het getal 0,58048... via een kettingbreuk benaderen met een breuk q/p,
betekent dit dat we om rein klinkende tertsen te krijgen een oktaaf moeten onderverdelen in p toetsen.
De q-de toets in deze reeks zal dan een kwint opleveren die net zoveel te klein is, dat de tertsen rein klinken.
Elke stap in de benadering noemt men een convergent en vormt een breukbenadering van het decimaal getal.
De noemer van deze breuk zegt ons in hoeveel we stappen we het octaaf moeten verdelen.
De teller zegt ons welke stap precies op de gewenste kwintverhouding uitkomt.

Breukbenaderingen uitgewerkt
We werken de breukbenaderingen uit in stapsgewijs steeds een betere benaderingen.

Deze benadering voldoet natuurlijk helemaal nog niet.
met een oktaaf dat slechts  in 2 stappen opgedeeld wordt geraak je niet ver.

Het gaat de goede richting uit, maar we moeten nog verder.

De breuk 4/7 is ons natuurlijk niet helemaal vreemd.
Hij komt neer op een diatonische toonladder van 7 stappen, waarbij het verschil tussen hele en halve tonen
is uitgevlakt. Hierin vormt de kwint de 4e stap.

De breuk 7/12 herkennen we natuurlijk.
Hij komt overeen met onze gelijkzwevende chromatische toonladder van 12 halve tonen.
Hierin vormt de kwint de 7e stap.

Een onderverdeling in 19 trappen werd theoretisch uitgewerkt in een 19-toonsverdeling, maar niet in praktijk gebracht.

Huygens vond achtereenvolgens de breuken: 1/2  3/5  4/7  7/12  11/19  18/31  101/174  119/205.
Huygens verkiest de verdeling van een oktaaf in 31 toontrappen, met de kwint als 18e stap.
Je kan een oktaaf onderverdelen in 205 stapjes, maar instrumenten maken met deze verdeling is wat anders.
Huygens stelt voor om een oktaaf in 31 toontrappen te verdelen,
zodat je op elk instrument muziek kan spelen in om het even welke toonaard.
Maar ook 31 lijkt een heksentoer. 31 toetsen naast elkaar maakt een klavier onbespeelbaar.
Joan Albert Ban, priester en bevriend met Descartes en Huyghens, ontwikkelde het "Volmaekte Klaeuwier".
Omdat de afstand tussen de tonen en de omvang niet te groot zou worden, ontwerpt hij tussenliggende toetsen
die boven elkaar liggen in verschillende rijen.

Niet alleen de kwintbenadering is mooi, ook de kwart en de terts van Huygens zijn heel knap.

toontrap	verhouding Huygens	verhouding rein	frequentie Huygens	frequentie rein	frequentie gelijkzwevend
kwint	2(18/31) = 1,4955	3/2 = 1,5	658 Hz	660 Hz	659 Hz
kwart	2(13/31) = 1,3373	4/3 = 1,333	588 Hz	587 Hz	587 Hz
terts	2(10/31) = 1,2505	5/4 = 1,25	550 Hz	550 Hz	554 Hz

Ban kon zo onzuiverheden opvangen zonder compromissen te doen, maar een succes werd zijn uitvinding niet.
Het instrument bleek toch niet zo praktisch.
7/12 is minder nauwkeurig dan 18/31, maar het bleek praktischer in het bouwen van instrumenten.