de kwinten van
Pythagoras
wiskunde-interactief.be
Het geheel rond sinusfuncties, geluid en
muziek is uitgewerkt op acht pagina's:
-
van
sinusfuncties tot een toonsysteem schetst
de natuurkundige en wiskundige basis van geluid.
-
samenklanken
en verhoudingen beluistert en onderzoekt
het resultaat van samenklinkende geluiden.
-
boventonen
en zwevingen onderzoekt
het voorkomen van natuurlijke boventonen en het
waarnemen
van zwevingenbij tonen die nauwelijks van elkaar verschillen.
-
de kwinten
van Pythagoras ontleedt hoe Pythagoras
vanuit kwintverhoudingen een toonladder opbouwt.
-
het komma
van Pythagoras' ontleedt hoe Pythagoras
vanuit kwintverhoudingen een toonladder opbouwt.
-
een
muzikale zoektocht' volgt de
muziekgeschiedenis in zijn zoektocht naar
welluidendheid.
- barokstemmingen'
ontleedt enkele pogingen om nieuwe oplossingen
te vinden voor nieuwe muzikale wensen.
-
de
kettingbreuk van Huygens' ontleedt Huygens'
berekeningen om een 'juister' klinkende
toonladder uit te bouwen.
Extra: partituurfragmenten en youtube-filmpjes
illustreren de theorie.
-
de zoektocht in klank en beeld:
opmerking over het afspelen
van geluid:
GeoGebra is in de eerste plaats een fantastisch
wiskundeprogramma maar geen gesofisticeerd
keyboard.
Verschijnt er bijvoorbeeld in een grijs scherm
een foutmelding over het afspelen, herlaad dan
gewoon de pagina en
klik gewoon opnieuw op 'speel'. Doe hetzelfde
wanneer je het afspelen van een geluid niet kan
stoppen.
Hoor je geen geluid, probeer dan eens een andere
browser...
Zelfs met deze gebreken is het een unieke manier
voor wiskundigen om iets over muziek te leren en
omgekeerd. |
Drie tonen
Omdat octaven en kwinten meeklinken in de natuurlijke boventoonreeks, vormen ze doorheen de geschiedenis
de basis van
toonstelsels.
Vanuit een do als grondtoon zijn de sol en de fa belangrijke tonen.
De grondtoon do noemen we toontrap I.
De sol (toontrap V) is de stijgende kwint van de grondtoon.
De fa(toontrap IV) is de dalende kwint van het octaaf.
Deze drie toontrappen I (do-C), IV (fa-F) en V (sol-G) vormen de basis van heel wat muziek.
Vraag het maar aan gitaristen. Met slechts drie akkoorden kan je heel wat
populaire muziek begeleiden.
In de toonaard van C (do) zijn dit C, F en G.
In de toonaard van G (sol) zijn dit G, C en D
De drie toontrappen I - IV en V vormen ook de basis voor de klassieke
harmonieleer.
Pentatonische toonladder
Zoals de naam doet vermoeden ('penta' is Grieks voor 5), is de pentatonische toonladder opgebouwd uit 5
tonen.
Stapel je vanaf de grondtoon C(do) 4 kwinten op elkaar, dan krijg je C - G - D -
A - E.
Herleid je die tonen naar eenzelfde oktaaf, dan krijg je de opeenvolging C - D -
E - G - A:

Een toonladder met 7 stamtonen
Pythagoras (6e eeuw v.C) is er van overtuigd dat alles in de natuur kan
beschreven worden in verhoudingen
van natuurlijke getallen.
Op de pagina sinus en geluid kan je lezen
dat Pythagoras zich baseerde op de
verhoudingen tussen de
frequenties van samenklinkende tonen.
De basisverhouding voor het toonsysteem is de frequentieverhouding 2 (=
octaafverhouding).
Pythagoras stelt ook vast dat de verhouding 3/2 heel welluidend is (=
kwintverhouding).
Deze twee verhoudingen gebruikt hij om het octaaf te verdelen.
Net zoals 'de vriend van mijn vriend is mijn vriend' stapelt hij kwintverhouding
op kwintverhouding.
De opbouw van het toonsysteem steunt dus op volgende bewerkingen:
- Een octaaf verhogen = . 2
- Een octaaf verlagen = : 2
- Een kwint verhogen = . 3/2
- Een kwint verlagen = : 3/2
Pythagoras vertrekt van een grondtoon en de verhouding
3/2 tot de kwint.
De kwint van de kwint wordt dan 3/2 x 3/2 enz.
Volg de opbouw van deze verdeling in onderstaand applet:
De opeenvolging van halve en hele tonen in onze toonladder
is dus niet zomaar een willekeurige keuze.
Ze is het gevolg van een verdeling vanuit reine kwintverhoudingen.
Zouden we de twee halve toonafstanden samenvoegen de octaafafstand verdelen in 6
hele toonafstanden,
dan zou de toon met frequentieverhouding 3/2 niet eens in de toonladder zitten,
terwijl ze juist de basis vormt.
Het denken in frequentieverhoudingen 2/1 en 3/2 is universeel en volgt uit het
voorkomen van boventonen.
De
verdeling van een octaaf in hele en halve toontrappen is geen keuze van
Pythagoras.
Ze is een gevolg de aanpak om het basisinterval te verdelen: het gebruiken van
de 3/2 verhouding.
Dit is een culturele keuze, net zoals het aantal stamtonen waarmee men werkt.
Wij zijn gewoon om melodielijnen te maken met 7 stamtonen. Het hadden er ook 5
of 8 of 9 kunnen zijn.
Stop je niet bij 7 tonen, dan kan je verder gaan tot het octaaf verdeeld is in
enkel halve toonafstanden.
Maar dan begint het bouwsel van frequentieverhoudingen te wankelen.
Uit een pianoklavier zou je kunnen afleiden dat een interval
van
12 kwinten gelijk is aan 7 octaven.
Want in kwintstappen belanden we na 12 kwinten op een si#.
Tussen si en do is maar een halve toon, dus de si# moet samenvallen met een do.

Maar dat blijkt toch niet zo mooi te kloppen als Pythagoras gehoopt had..
Want de frequentieverhouding van 12 kwinten wordt (2)7=128
en die van 7 octaven (3/2)12
= 129.7.
Binnen een octaaf is deze afwijking zo gering dat de 3/2- verhouding als perfect
welluidend wordt ervaren.
Het probleem stelt zich bij wel bij het blijvend opeenstapelen van kwinten.
En ook binnen een octaaf heeft het zware gevolgen.
Zo wordt de terts berekend vanuit 4 opeengestapelde kwintverhoudingen.
Omdat hierbij ook de (geringe) afwijkingen opgeteld worden, zal de terts hoorbaar te
hoog klinken.
De tertsverhouding 81/64 (= 1.2656) klinkt niet
welluidend,
want die breuk komt niet voor in de reeks
van natuurlijke boventonen.
In deze reeks komt wel de verhouding 5/4 (= 1.25)
voor t.o.v. de
grondtoon.
Pythagoras negeerde daarom zijn terts en steunde enkel op kwinten
en octaven.
Oeps... een probleempje!
(of waarom een stapeling van kwinten niet in een geheel
aantal octaven past...)
Tel je in trappen van halve tonen van grondtoon tot
octaaf, dan krijg je volgende reeks:
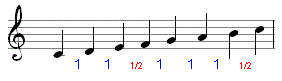
do - do# - re - re# - mi - fa - fa# - sol - sol# - la - la# - si - do.
In deze reeks is de kwint (sol) de 7e trap van 12. en een octaaf de 12e trap.
Wanneer we spreken over ‘de kwint van de kwint van een grondtoon’, zeggen we dat
we kwinten optellen.
Maar hiermee begeven we ons op glad ijs. Wiskundig zijn we immers helemaal niet
aan het optellen,
maar vermenigvuldigen we een frequentie met een factor 3/2.
Dit is geen taalpurisme maar maakt een fundamenteel verschil.
Bij optellen tel je lineair, bij vermenigvuldigen exponentieel. We plaatsen
beide modellen eens naast elkaar.
lineair model:
In gelijke stapjes van 0 tot 12 tellen we met elke toontrap
telkens 1/12 bij.
| do |
do# |
re |
re# |
mi |
fa |
fa# |
sol |
sol# |
la |
la# |
si |
do |
| 0
|
1/12
|
2/12
|
3/12
|
4/12
|
5/12
|
6/12
|
7/12
|
8/12
|
9/12
|
10/12
|
11/12
|
12/12 =
1 |
exponentieel model:
De frequentie van het octaaf is 2 maal deze van de grondtoon.
Bij elke toontrap van een halve toon vermenigvuldigen we de frequentie met 2(1/12) .
We rekenen dus in een exponentieel verband met groeifactor 2(1/12).
| do |
do# |
re |
re# |
mi |
fa |
fa# |
sol |
sol# |
la |
la# |
si |
do |
| 1
|
21/12
|
22/12
|
23/12
|
24/12
|
25/12
|
26/12
|
27/12
|
28/12
|
29/12
|
210/12
|
211/12
|
212/12 = 2 |
Rekenen we met stappen van octaven, dan is er een
exponentieel verband met groeifactor 2.
n octaven hebben verhouding van
2n
ten opzichte van de grondtoon.
Een reine kwint heeft een verhouding 3/2 ten opzichte van de
grondtoon.
Rekenen we met stappen van kwinten, dan is er een exponentieel verband met
groeifactor 3/2.
n kwinten hebben een verhouding
(3/2)n
ten opzichte van de grondtoon.
Elke wiskundige weet dat een macht van 3 altijd oneven is, en dus nooit
gelijk zal zijn aan een macht van 2.
Een geheel aantal kwinten (verhouding 3/2) kan dus nooit gelijk zijn aan een
geheel aantal octaven (verhouding 2/1).
|
De
verhouding tussen 12 kwinten en 7 octaven noemt men
het
komma van Pythagoras.
|
312 |
: |
27 |
= |
531441 |
: 128 = |
531441
|
= |
531441 |
=1,0136 |
| 212 |
17 |
4096 |
4096
. 128 |
524288 |
Met andere woorden: 12 reine kwinten = 1,0136 keer 7
reine octaven |
In ons toonsysteem komen we na 12
kwintstappen uit op een si#.
| stapgrootte |
stappen |
verhouding |
| kwinten |
do . . . sol . . . re . . .
la . . mi . . . si . . . fa# . . . do# . .
. sol# . . . re# . . . la# . . . mi# . . . si#
|
(3/2)12
= 129,75 |
| octaven |
do . . . . . .
do. . . . . . do. . . . . .
do. . . . . . do. . . . . .
do. . . . . . do. . . .
. . do |
(2/1)7
= 128 |
In ons toonsysteem is een do is een halve noot hoger dan een si. Een si# zou dus
gelijk moeten zijn aan een do.
Maar rekenend in kwinten komen we iets hoger uit dan rekenend in octaven.
Is dat nu een probleem: één kommaatje na 7 octaven?
Voor eenvoudige liedjes is dat inderdaad geen enkel probleem, maar wanneer je
binnen één muziekstuk het tooncentrum
wil verleggen (= moduleren), ja dan kom je echt wel in de problemen. Want, al
kom je een si# nog niet zo snel tegen,
een si# die verschilt van een do doet heel het systeem wankelen.
Want een la b is dan ook niet gelijk aan een sol#, een fa# niet aan een sol b enz.
Hoe het komt dat een la b niet gelijk is aan een sol# kunnen we illustreren door
de kwintenrij uit te breiden:
Ab - Eb -
Bb - F - C
- G - D - A - E - B
- F# - C# -
G#
-4
-3
-2 -1
1 2 3
4 5 6
7 8
De Ab vinden we 4 kwinten onder de C. Deze herleiden we vervolgens naar het
basisoctaaf van de centrale C.
De verhouding van deze Ab en de grondtoon C = 1 : (3/2)4
. 23 =
1,5802
De G# vinden we 8 kwinten boven de C. Deze herleiden we vervolgens naar het
basisoctaaf van de centrale C.
De verhouding van deze G# en de grondtoon C = (3/2)8
: 24
=
1,6018
De G# ligt dus iets hoger dan de Ab. Het verschil tussen beide tonen vinden we
als de verhouding
1,6018 / 1,5802 =
1,01367 en is dus gelijk aan het komma van
Pythagoras (iets meer dan 1/9 van een hele toon).
Speel je b.v muziek in de toonaarden Eb groot of c (do klein) dan moet je
eigenlijk een Ab spelen.
Speel je in de toonaarden A of E dan moet je een G# spelen en dat wordt moeilijk
wanneer op een klavier
voor de twee verschillende tonen slechts een toets voorzien wordt. Je hebt dan 3
mogelijkheden:
- Ofwel maak je de keuze om slechts een van beide juist te stemmen.
- Ofwel kies je voor het midden van beide tonen en speel je ze allebei een
beetje onzuiver.
- Ofwel bouw je een klavier met aparte toetsen voor de twee tonen.

Zo beschreef Michael Praetorius in 1619 het zogenaamde 'cembalo universale' met
opgesplitste toetsen en ook
in historische beschrijvingen van kerkorgels is sprake van dergelijke klavieren.
Kwinten en tertsen
Het verhaal van kwinten en tertsen is een gelijkaardig verhaal.
Vanuit kwinten een breukverhouding vinden voor tertsen lijkt een eenvoudige som
van breuken.
En weer is het rekenen met machten de reden dat ook dit niet lukt.
lineair model:
| do |
do# |
re |
re# |
mi |
fa |
fa# |
sol |
sol# |
la |
la# |
si |
do |
| 0
|
1/12
|
2/12
|
3/12
|
4/12
|
5/12
|
6/12
|
7/12
|
8/12
|
9/12
|
10/12
|
11/12
|
12/12 =
1 |
In de chromatische toonladder is de terts (mi) de 4e trap en de
kwint (sol)
de 7e.
Je vindt gemakkelijk hoe een geheel aantal kwinten kan samenvallen met een
geheel aantal tertsen
door de twee schuifknoppen te verslepen.
exponentieel model:
Een reine kwint heeft een verhouding 3/2 ten opzichte van de
grondtoon.
Rekenen we met stappen van kwinten, dan is er een exponentieel verband met
groeifactor 3/2.
n kwinten hebben een verhouding
(3/2)n
ten opzichte van de grondtoon.
Een reine terts heeft een verhouding 5/4 ten opzichte van de
grondtoon.
Rekenen we met stappen van kwinten, dan is er een exponentieel verband met
groeifactor 5/4.
n tertsen hebben dus een verhouding
(5/4)n
ten opzichte van de grondtoon.
Ook 5 en 3 zijn onderling ondeelbaar.
Een macht van 3 zal nooit gelijk zal zijn aan een macht van 5.
Een geheel aantal tertsen (verhouding 5/4) kan dus nooit gelijk zijn aan een
geheel aantal kwinten (verhouding 3/2).
De 4 kwinten komen hoger uit dan de 7 tertsen.
Wanneer we de terts berekenen vanuit gestapelde kwinten krijgen we als
verhouding (3/2)4: 4 = 81/64 = 1,2656
Een reine terts heeft als verhouding 5/4 = 1,25.
De verhouding tussen beide noemen we het
syntonische komma.
|
De
verhouding tussen de terts, berekend vanuit gestapelde
kwinten, en de reine terts
noemt men het syntonische komma.
| 81 |
: |
5 |
= |
81 .
4 |
= |
81 |
= 1,0125 of
ongeveer 1/9 van een
hele toonafstand. |
| 64 |
4 |
64 .
5 |
80 |
Met andere woorden: 4 reine kwinten = 1,0125 keer 7
reine tertsen |
Een onoplosbaar probleem
Pythagoras, die dol was op natuurlijke verhoudingen, werkte van uit deze
verhoudingen een toonsysteem uit.
Maar... een toonsysteem maken waarin zowel octaven, kwinten als tertsen rein
klinken, blijkt onmogelijk.
Het was een mooie droom.
De getallen 2, 3 en 5 zijn onderling ondeelbaar. Machten van 3 en machten van 5
komen nooit overeen met
machten van 2. Een stapeling van kwinten of tertsen komt dus nooit overeen met
een geheel aantal octaven.
De muziekgeschiedenis kan je op verschillende manieren lezen.
Een manier is het volgen van de muzikale en wiskundige zoektocht naar
welluidendheid. Anders geformuleerd:
Hoe verdeel je een octaaf in de wetenschap dat
terts, kwint en octaaf samen nooit rein kunnen zijn?
De reine stemming
Reeds rond 300 v.C werden alternatieven bedacht voor de stemming van Pythagoras.
De terts wordt niet meer berekend vanuit opeengestapelde kwinten maar
rechtstreeks vanuit de verhouding 5/4.
Ook sext en septiem worden niet meer berekend vanuit de kwint, maar vanuit deze
terts.
| toontrap |
berekening
door kwinten en tertsen |
verhouding
frequenties |
frequentie
vanuit la = 440 Hz |
| prime (C) |
C |
1/1 |
1/1 |
440 Hz |
| secunde (D)
|
C - G - D
2x kwint : 1 oktaaf terug |
3/2 x 3/2 : 2 |
9/8 |
495 Hz |
| terts (E) |
C - E
1xterts |
5/4 |
5/4 |
550 Hz |
| kwart (F) |
F - C
dalende kwint van oktaaf |
2 : 3/2 |
4/3 |
587 Hz |
| kwint (G) |
C - G |
3/2 |
3/2 |
660 Hz |
| sext (A) |
C - E - A
1x terts en 1x kwart |
5/4 x 4/3 |
5/3 |
733 Hz |
| septime (B) |
C - E - B
1x terts en 1x kwint
|
5/4 x 3/2
|
15/8 |
825 Hz |
| octaaf (C) |
C - C |
2/1 |
2/1 |
880 Hz |
De breuken in de frequentieverhoudingen zijn eenvoudiger dan bij Pythagoras.
De verhoudingen van de verschillende toontrappen met als grondtoon do worden nu:
Er duiken echter nieuwe problemen op:
- Omdat A verlaagd is (want vanuit de terts berekend) en D niet, is dan de kwint
D - A niet meer rein.
-
Niet alle hele toonsafstanden zijn gelijk. Dat is ook logisch.
Secunde, kwart en kwint (de grijze toetsen,) zijn berekend vanuit iets te grote
kwintverhoudingen.
Terts, sext en septiem (de groene toetsen) zijn berekend vanuit de iets kleinere
tertsverhouding.
Resultaat is:
- Hele toonafstanden tussen toetsen van dezelfde kleur hebben een gelijke
toonafstand: de verhouding 9/8.
- Volgt een groene toets (lagere tertstoon) op een grijze (hogere kwinttoon) dan
is de afstand kleiner: 10/9.
We spreken daarom van grote hele tonen en
kleine hele
tonen.
De verhouding tussen een grote en een kleine hele toon is gelijk aan 9/8 : 10/9
= 9/8 . 9/10 = 81/80.
Deze verhouding noemen we het syntonische komma.
- De twee halve tonen zijn gelijk. In beide gevallen volgt een grijze toets op
een groene.
De terts klinkt nu wel welluidend en rein, maar dat alle hele tonen niet gelijk
zijn, heeft verstrekkende gevolgen.
Want hoe groot zijn bijvoorbeeld de toonafstanden sol-la en la-si?
|
in toonaard van C:
|
do |
re |
mi |
fa |
sol |
|
la |
|
si |
do |
|
| 1 |
2 |
3 |
4 |
5 |
|
6 |
|
7 |
8 |
|
| |
|
|
|
|
|
klein |
|
groot |
|
|
De afstand sol - la is een
kleine hele noot.
De afstand la - si is een grote hele noot |
|
in toonaard van G:
|
sol |
|
la |
|
si |
do |
re |
mi |
fa |
sol |
|
| 1 |
|
2 |
|
3 |
4 |
4 |
6 |
7 |
8 |
|
| |
|
groot |
|
klein |
|
|
|
|
|
|
De afstand sol - la is een
grote hele noot.
De afstand la - si is een kleine hele noot |
In de reine toonladder is de afstand tussen twee tonen dus afhankelijk van de
toonladder.
Stem je een instrument in de toonaard van C en speel je hierop muziek in andere
toonaarden, dan zullen
de onderlinge verhoudingen heel anders liggen en zal de muziek afschuwelijk vals
klinken.
Een ander probleem vormen de tussenliggende halve tonen (de zwarte toetsen op de
piano).
De verhoudingen van deze tonen berekent men door in kwinten en tertsen verder te
rekenen vanuit de
andere stamtonen.
Rekent men vanuit stijgende kwinten, dan verschijnen de kruisen (verhogingsteken
#).
Rekent men vanuit dalende kwinten dan verschijnen de mollen (verlagingsteken b).
En o ramp, de verlaagde toon komt iets lager uit dan het midden van de hele
toon, de verhoogde toon iets hoger.
Met andere woorden: de Bb (simol) is iets lager dan de A#(lakruis).
We kunnen moeilijk klavieren maken met telkens twee zwarte toetsen tussen een
hele noot.
De reine stemming vormt geen probleem zolang je binnen een toonaard blijft.
Muziek uit de middeleeuwen en de renaissance verandert daarom niet midden in een
stuk en de gebruikte
toonaarden waarin gecomponeerd werd, bleven beperkt.
Blokfluitmuziek voor een instrument in do werd dan ook in do geschreven en niet
in fa of la.
Vergelijking van de verschillende stemmingen
Wanneer we de verdeling van het octaaf grafisch uitzetten, zie je de verschillen
tussen de stemmingen
van Pythagoras, de reine en onze hedendaagse stemming (de gelijkzwevende stemming).
De grootste verschillen zitten duidelijk in de terts, de sext en de septime.
In het onderstaande applet zie je drie mini-toetsenbordjes met enkel de witte
toetsen.
Hoe hoorbaar de verschillen zijn tussen de toontrappen in de verschillende
stemmingen,
kan je nagaan door te klikken op de toetsen.


