berekenen van inhouden
wiskunde-interactief.be
Berekenen van inhouden
In de meetkunde kennen we zogenaamde omwentelingslichamen:
Door de som te maken van rechthoekjes benaderden we reeds oppervlakten.
Wanneer we deze rechthoekjes wentelen rond de x-as, benaderen we
omwentelingslichamen
door een reeks dunne schijfjes.
De inhoud van een schijfje is de inhoud van een cilinder.
De inhoudsformule van een cilinder is
V =
S . h = π
. r2.
h
De straal van deze cilinder komt overeen met de functiewaarde f(x) = y
S(x) =
π.
y2
De inhoud van het omwentelingslichaam is de som van al deze kleine inhoudjes.
De totale inhoud van een omwentelingslichaam van ondergrens a tot bovengrens b
bereken je als:
| V =
|
b |
|
b |
|
| ∫ |
S(x) dx =
π
.
|
∫ |
y2 dx
|
| a |
|
a |
|
|
Toepassing: inhoud van een bolschijf
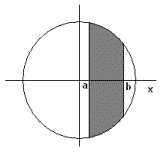 |
inhoud van een bolschijf
Van een bol met straal r bereken we de inhoud van een
bolschijf
met als ondergrens a en als bovengrens b.
We spreken van een bolsegment als de bovengrens
gelijk is aan de straal.
Een cirkel heeft als vergelijking x2 + y2
= r2.
Wanneer we een cirkel wentelen rond zijn diameter krijgen we een
bol.
In de integraalformule voor inhouden kunnen we nu gemakkelijk y2
invullen.
We berekenen de inhoud van de bolschijf met de volgende
formule:
|
Inhoud van een kegel
Met de inhoudformule voor omwentelingslichamen vind je ook de formule van een
kegel terug:
in 3d wentelen we de eerstegraadsfunctie met voorschrift f(x) = x rond de x-as:
Inhoud van een bol
Vanuit de vergelijking van een cirkel
kunnen we de inhoud van een bol afleiden:
in 3d vinden we bol, bolschijf en bolsegment:
Inhoud van een torus
Teken een cirkel met middelpunt buiten de x-as en wentel hem rond de x-as.
Het resultaat ken je misschien beter als een donut.
Een colaflesje tekenen in 3D
We proberen eerst de vorm van een flesje te benaderen door een veeltermfunctie:
- We tekenen eerst enkele punten op een afbeelding van een flesje
- We berekenen de veeltermfunctie die het dichtst deze punten benadert
door het commando VeeltRegr[<lijst van punten>,<graad>].
We wentelen dan deze grafiek rond de x-as, wat een 3D-vorm oplevert.
